
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 232 Атанасян — Подробные Ответы
Диагональ прямоугольного параллелепипеда, равная \(d\), образует с плоскостью основания угол \(\varphi\), а с одной из боковых граней — угол \(\psi\). Найдите площадь боковой поверхности параллелепипеда
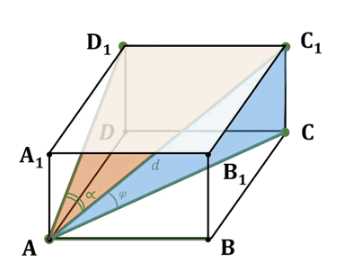
Дано: \( ABCD A_1B_1C_1D_1 \) — прямоугольный параллелепипед, \( AC_1 = d \), \( \angle CA C_1 = \phi \), \( \angle D_1 AC_1 = \alpha \).
Обозначим стороны: \( AB = x \), \( AD = y \), \( AA_1 = z \).
По свойствам параллелепипеда:
\( x = d \cdot \sin(\alpha) \),
\( z = d \cdot \sin(\phi) \).
По теореме Пифагора:
\( y = \sqrt{d^2 — d^2 \cdot \sin^2(\alpha) — d^2 \cdot \sin^2(\phi)} = d \cdot \sqrt{1 — \sin^2(\alpha) — \sin^2(\phi)} \).
Площадь боковой поверхности:
\( S_{\text{бок}} = 2 \cdot (x + y) \cdot z \).
Подставляем:
\( S_{\text{бок}} = 2 \cdot d \cdot (\sin(\alpha) + \sqrt{1 — \sin^2(\alpha) — \sin^2(\phi)}) \cdot d \cdot \sin(\phi) \).
Ответ:
\( S_{\text{бок}} = 2 \cdot d^2 \cdot (\sin(\alpha) + \sqrt{1 — \sin^2(\alpha) — \sin^2(\phi)}) \cdot \sin(\phi) \).
Дано прямоугольный параллелепипед \(ABCD A_1B_1C_1D_1\), в котором диагональ \(AC_1 = d\), угол между диагональю и ребром \(AC_1\) равен \(\phi\), угол между диагональю и ребром \(D_1A\) равен \(\alpha\). Требуется найти площадь боковой поверхности \(S_{\text{бок}}\).
Обозначим стороны параллелепипеда следующим образом: \(AB = x\), \(AD = y\), \(AA_1 = z\).
Сначала выразим \(x\), \(y\) и \(z\) через диагональ \(d\) и углы \(\alpha\), \(\phi\). Так как треугольники \(ACA_1\) и \(AD_1A_1\) прямоугольные, по определению синуса:
\(x = d \cdot \sin(\alpha)\), так как \(x\) является противолежащим катетом угла \(\alpha\) в треугольнике \(ACA_1\).
\(z = d \cdot \sin(\phi)\), так как \(z\) является противолежащим катетом угла \(\phi\) в треугольнике \(AD_1A_1\).
Теперь найдем \(y\) — третью сторону параллелепипеда. Для этого используем теорему Пифагора для диагонали \(AC_1\), которая проходит через три стороны \(x\), \(y\) и \(z\):
\(x^2 + y^2 + z^2 = d^2\).
Подставим выражения для \(x\) и \(z\):
\((d \cdot \sin(\alpha))^2 + y^2 + (d \cdot \sin(\phi))^2 = d^2\).
Раскроем квадраты:
\(d^2 \cdot \sin^2(\alpha) + y^2 + d^2 \cdot \sin^2(\phi) = d^2\).
Вынесем \(y^2\):
\(y^2 = d^2 — d^2 \cdot \sin^2(\alpha) — d^2 \cdot \sin^2(\phi)\).
Вынесем общий множитель \(d^2\):
\(y^2 = d^2 \cdot (1 — \sin^2(\alpha) — \sin^2(\phi))\).
Возьмем корень из обеих частей:
\(y = d \cdot \sqrt{1 — \sin^2(\alpha) — \sin^2(\phi)}\).
Теперь найдем площадь боковой поверхности \(S_{\text{бок}}\). Боковая поверхность состоит из двух одинаковых прямоугольников с размерами \(z\) и \(x + y\). Таким образом:
\(S_{\text{бок}} = 2 \cdot (x + y) \cdot z\).
Подставим выражения для \(x\), \(y\) и \(z\):
\(S_{\text{бок}} = 2 \cdot (d \cdot \sin(\alpha) + d \cdot \sqrt{1 — \sin^2(\alpha) — \sin^2(\phi)}) \cdot d \cdot \sin(\phi)\).
Вынесем \(d^2\) за скобки:
\(S_{\text{бок}} = 2 \cdot d^2 \cdot (\sin(\alpha) + \sqrt{1 — \sin^2(\alpha) — \sin^2(\phi)}) \cdot \sin(\phi)\).
Таким образом, окончательный ответ:
\(S_{\text{бок}} = 2 \cdot d^2 \cdot (\sin(\alpha) + \sqrt{1 — \sin^2(\alpha) — \sin^2(\phi)}) \cdot \sin(\phi)\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!