
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 231 Атанасян — Подробные Ответы
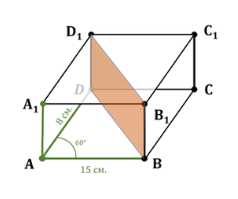
Стороны основания прямого параллелепипеда равны 8 см и 15 см и образуют угол в \(60^\circ\). Меньшая из площадей диагональных сечений равна 130 см\(^2\). Найдите площадь поверхности параллелепипеда.
Дан прямой параллелепипед. Найдем диагональ основания \(BD\) по теореме косинусов:
\(BD^2 = AB^2 + AD^2 — 2 \cdot AB \cdot AD \cdot \cos(\angle BAD)\),
\(BD^2 = 15^2 + 8^2 — 2 \cdot 15 \cdot 8 \cdot 0.5 = 169\),
\(BD = \sqrt{169} = 13 \, \text{см}\).
Высота \(h\) диагонального сечения:
\(S_{B_1B_1D_1D} = BD \cdot h \Rightarrow h = \frac{130}{13} = 10 \, \text{см}\).
Площадь поверхности:
\(S_{\text{поверхности}} = S_{\text{бок}} + 2 \cdot S_{\text{осн}}\),
\(S_{\text{бок}} = P \cdot h = 2 \cdot (AB + AD) \cdot h = 2 \cdot (15 + 8) \cdot 10 = 460 \, \text{см}^2\),
\(S_{\text{осн}} = AB \cdot AD \cdot \sin(\angle BAD) = 15 \cdot 8 \cdot \frac{\sqrt{3}}{2} = 60 \cdot \sqrt{3} \, \text{см}^2\),
\(S_{\text{поверхности}} = 460 + 2 \cdot 60 \cdot \sqrt{3} = 460 + 120 \cdot \sqrt{3} \, \text{см}^2\).
Ответ: \(S_{\text{поверхности}} = 460 + 120 \cdot \sqrt{3} \, \text{см}^2\).
Дан прямой параллелепипед \(ABCDA_1B_1C_1D_1\), где \(AB = 15 \, \text{см}\), \(AD = 8 \, \text{см}\), угол \(\angle BAD = 60^\circ\), а площадь диагонального сечения \(S_{B_1B_1D_1D} = 130 \, \text{см}^2\). Нужно найти площадь полной поверхности \(S_{\text{поверхности}}\).
Сначала находим диагональ основания \(BD\) с использованием теоремы косинусов. По теореме косинусов для треугольника \(ABD\):
\(BD^2 = AB^2 + AD^2 — 2 \cdot AB \cdot AD \cdot \cos(\angle BAD)\).
Подставляем значения:
\(BD^2 = 15^2 + 8^2 — 2 \cdot 15 \cdot 8 \cdot \cos(60^\circ)\).
Так как \(\cos(60^\circ) = 0.5\), получаем:
\(BD^2 = 225 + 64 — 2 \cdot 15 \cdot 8 \cdot 0.5 = 225 + 64 — 120 = 169\).
Находим \(BD\):
\(BD = \sqrt{169} = 13 \, \text{см}\).
Поскольку диагональ \(BD\) лежит напротив меньшего угла \(\angle BAD\), она является меньшей диагональю в основании параллелепипеда.
Далее определяем высоту \(h\) диагонального сечения. Площадь диагонального сечения \(S_{B_1B_1D_1D}\) равна произведению диагонали \(BD\) на высоту \(h\):
\(S_{B_1B_1D_1D} = BD \cdot h\).
Подставляем значения:
\(130 = 13 \cdot h\).
Находим \(h\):
\(h = \frac{130}{13} = 10 \, \text{см}\).
Теперь вычисляем площадь полной поверхности параллелепипеда. Полная поверхность состоит из боковых граней и двух оснований. Площадь боковых граней равна произведению периметра основания \(P\) на высоту \(h\):
\(S_{\text{бок}} = P \cdot h\),
где \(P = 2 \cdot (AB + AD)\). Подставляем значения:
\(P = 2 \cdot (15 + 8) = 2 \cdot 23 = 46 \, \text{см}\).
Тогда:
\(S_{\text{бок}} = 46 \cdot 10 = 460 \, \text{см}^2\).
Площадь каждого основания равна \(S_{\text{осн}} = AB \cdot AD \cdot \sin(\angle BAD)\). Подставляем значения:
\(S_{\text{осн}} = 15 \cdot 8 \cdot \sin(60^\circ)\).
Так как \(\sin(60^\circ) = \frac{\sqrt{3}}{2}\), получаем:
\(S_{\text{осн}} = 15 \cdot 8 \cdot \frac{\sqrt{3}}{2} = 60 \cdot \sqrt{3} \, \text{см}^2\).
Площадь двух оснований равна:
\(2 \cdot S_{\text{осн}} = 2 \cdot 60 \cdot \sqrt{3} = 120 \cdot \sqrt{3} \, \text{см}^2\).
Суммируем площади боковых граней и оснований:
\(S_{\text{поверхности}} = S_{\text{бок}} + 2 \cdot S_{\text{осн}}\).
Подставляем значения:
\(S_{\text{поверхности}} = 460 + 120 \cdot \sqrt{3} \, \text{см}^2\).
Ответ:
\(S_{\text{поверхности}} = 460 + 120 \cdot \sqrt{3} \, \text{см}^2\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!