ГДЗ по Геометрии 10 класс Номер 230 Атанасян — Подробные Ответы

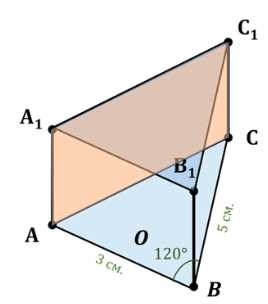
Основание прямой призмы — треугольник со сторонами 5 см и 3 см и углом в \(120^\circ\) между ними. Наибольшая из площадей боковых граней равна 35 см\(^2\). Найдите площадь боковой поверхности призмы

Дано: \(AB = 3 \, \text{см}, BC = 5 \, \text{см}, \angle ABC = 120^\circ, S_{\text{AA}_1C_1C} = 35 \, \text{см}^2\).

1. Найдем \(AC\) по теореме косинусов:
\(
AC^2 = AB^2 + BC^2 — 2 \cdot AB \cdot BC \cdot \cos(120^\circ)
\)
\(
AC^2 = 3^2 + 5^2 — 2 \cdot 3 \cdot 5 \cdot \left(-\frac{1}{2}\right) = 9 + 25 + 15 = 49
\)
\(
AC = \sqrt{49} = 7 \, \text{см}
\)

2. Найдем высоту \(h\):
\(
h = S_{\text{AA}_1C_1C} / AC = 35 / 7 = 5 \, \text{см}
\)

3. Периметр основания \(P = AB + BC + AC = 3 + 5 + 7 = 15 \, \text{см}\).

4. Площадь боковой поверхности:
\(
S_{\text{бок}} = P \cdot h = 15 \cdot 5 = 75 \, \text{см}^2
\)

Ответ: \(S_{\text{бок}} = 75 \, \text{см}^2\).

Дано: \(AB = 3 \, \text{см}, BC = 5 \, \text{см}, \angle ABC = 120^\circ, S_{\text{AA}_1C_1C} = 35 \, \text{см}^2\). Требуется найти площадь боковой поверхности призмы \(S_{\text{бок}}\).

Сначала найдем длину стороны \(AC\) треугольника \(ABC\) с использованием теоремы косинусов. Формула для нахождения стороны через две известные стороны и угол между ними выглядит так:
\(
AC^2 = AB^2 + BC^2 — 2 \cdot AB \cdot BC \cdot \cos(\angle ABC)
\)
Подставим значения:
\(
AC^2 = 3^2 + 5^2 — 2 \cdot 3 \cdot 5 \cdot \cos(120^\circ)
\)
Зная, что \(\cos(120^\circ) = -\frac{1}{2}\), получаем:
\(
AC^2 = 9 + 25 — 2 \cdot 3 \cdot 5 \cdot \left(-\frac{1}{2}\right)
\)
\(
AC^2 = 9 + 25 + 15 = 49
\)
\(
AC = \sqrt{49} = 7 \, \text{см}
\)

Теперь определим высоту призмы \(h\). Для этого используем формулу площади боковой грани \(S_{\text{AA}_1C_1C}\), которая равна произведению основания на высоту:
\(
S_{\text{AA}_1C_1C} = AC \cdot h
\)
Выразим \(h\):
\(
h = \frac{S_{\text{AA}_1C_1C}}{AC}
\)
Подставим известные значения:
\(
h = \frac{35}{7} = 5 \, \text{см}
\)

Теперь рассчитаем периметр основания призмы \(P\). Основание призмы — треугольник \(ABC\), поэтому его периметр равен сумме длин сторон:
\(
P = AB + BC + AC
\)
Подставим значения:
\(
P = 3 + 5 + 7 = 15 \, \text{см}
\)

Площадь боковой поверхности призмы \(S_{\text{бок}}\) равна произведению периметра основания на высоту:
\(
S_{\text{бок}} = P \cdot h
\)
Подставим значения:
\(
S_{\text{бок}} = 15 \cdot 5 = 75 \, \text{см}^2
\)

Ответ: \(S_{\text{бок}} = 75 \, \text{см}^2\).