Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 228 Атанасян — Подробные Ответы
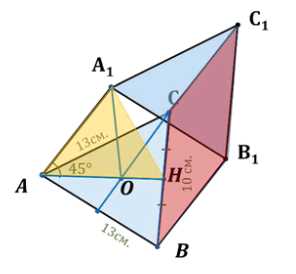
Основанием наклонной призмы \(ABCA_1B_1C_1\) является равнобедренный треугольник \(ABC\), в котором \(AC = AB = 13\) см, \(BC = 10\) см, а боковое ребро призмы образует с плоскостью основания угол в \(45^\circ\). Проекцией вершины \(A_1\) является точка пересечения медиан треугольника \(ABC\). Найдите площадь грани \(CC_1B_1B\).
Дан треугольник \( \triangle ABC \) с \( AB = AC = 13 \, \text{см} \) и \( BC = 10 \, \text{см} \). Угол между \( AA_1 \) и плоскостью \( ABC \) равен \( 45^\circ \). Найти площадь \( S_{CC_1B_1B} \).
Рассмотрим \( \triangle ABC \). Он равнобедренный, поэтому медиана, проведенная к основанию \( BC \), является высотой. Следовательно, \( BC \perp HA = CH = 5 \, \text{см} \).
Применяем теорему Пифагора к \( \triangle AHC \):
\(
AH^2 = AC^2 — CH^2 = 13^2 — 5^2 = 144 \Rightarrow AH = 12 \, \text{см}
\)
Точка пересечения медиан делит медиану в отношении 2:1, поэтому
\(
AO = \frac{2}{3} AH = 8 \, \text{см}
\)
Рассмотрим \( \triangle A_1OA \). Он равнобедренный и прямоугольный, следовательно,
\(
A_1O = 8 \, \text{см}, \quad A_1A = 8 \sqrt{2} \, \text{см}
\)
Используя аналогичные рассуждения, получаем, что \( CC_1B_1B \) — прямоугольник, и
\(
S_{CC_1B_1B} = BC \cdot A_1A = 10 \cdot 8\sqrt{2} = 80\sqrt{2} \, \text{см}^2
\)
Ответ: \( S_{CC_1B_1B} = 80\sqrt{2} \, \text{см}^2 \).
Дан треугольник ABC, который является равнобедренным, так как AB = AC = 13 см, а основание BC = 10 см. Точка пересечения медиан O делит медианы в отношении 2:1. Угол между высотой призмы AA₁ и плоскостью основания ABC равен 45°. Необходимо найти площадь боковой грани CC₁B₁B.
Для начала рассмотрим треугольник ABC. Так как он равнобедренный, медиана AH, проведенная к основанию BC, является также высотой. Это значит, что BC перпендикулярно AH, а точка H — середина отрезка BC. Следовательно, длины отрезков HA и CH равны и составляют 5 см.
Применяем теорему Пифагора к треугольнику AHC. Катеты в этом треугольнике — CH и AH, а гипотенуза — AC. Подставляем известные значения:
AC² = AH² + CH²
13² = AH² + 5²
169 = AH² + 25
AH² = 144
AH = 12 см
Теперь определим длину отрезка AO. Поскольку точка пересечения медиан делит медиану в отношении 2:1, длина AO равна двум третям от AH:
AO = (2/3) * AH = (2/3) * 12 = 8 см
Рассмотрим треугольник A₁OA. Этот треугольник является прямоугольным, так как AA₁ перпендикулярно плоскости основания ABC. В этом треугольнике гипотенуза — это AA₁, катеты — AO и A₁O. Угол между AA₁ и плоскостью основания равен 45°. Из геометрических соотношений в прямоугольном треугольнике с углом 45° следует, что катеты AO и A₁O равны. Таким образом, A₁O = AO = 8 см. Длина AA₁ определяется как:
AA₁ = A₁O * √2 = 8 * √2 см
Теперь рассмотрим боковую грань CC₁B₁B. Эта грань является прямоугольником, одна из сторон которого равна длине основания BC, а другая сторона равна длине AA₁. Площадь прямоугольника вычисляется по формуле:
S = BC * AA₁
S = 10 * 8√2
S = 80√2 см²
Таким образом, площадь боковой грани CC₁B₁B равна 80√2 см².
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.