
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 224 Атанасян — Подробные Ответы
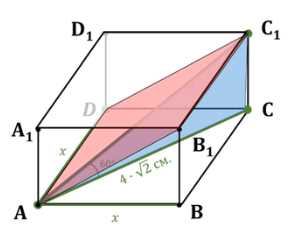
Диагональ правильной четырёхугольной призмы наклонена к плоскости основания под углом \(60^\circ\). Найдите площадь сечения, проходящего через сторону нижнего основания и противолежащую сторону верхнего основания, если диагональ основания равна \(4\sqrt{2}\) см.
Дано правильная призма \(ABCDA_1B_1C_1D_1\), основание которой — квадрат. Диагональ основания равна \(AC = 4\sqrt{2}\), а угол между диагональю боковой грани и плоскостью основания \(\angle(AC_1, ABC) = 60^\circ\). Сторона квадрата основания \(x\) находится из формулы диагонали квадрата: \(AC = x\sqrt{2}\). Подставляя \(AC = 4\sqrt{2}\), получаем \(x = 4\).
Высота призмы \(CC_1\) определяется из соотношения \(\tan(60^\circ) = \frac{CC_1}{AC}\). Подставляя значения, находим: \(CC_1 = AC \cdot \tan(60^\circ) = 4\sqrt{2} \cdot \sqrt{3} = 4\sqrt{6}\).
Диагональ боковой грани \(AB_1\) вычисляется по теореме Пифагора: \(AB_1^2 = AB^2 + B_1B^2 = 4^2 + (4\sqrt{6})^2 = 16 + 96 = 112\), откуда \(AB_1 = \sqrt{112} = 4\sqrt{7}\).
Площадь четырехугольника \(ADC_1B_1\) равна произведению диагонали \(AB_1\) на сторону основания \(AD\): \(S_{ADC_1B_1} = AB_1 \cdot AD = 4\sqrt{7} \cdot 4 = 16\sqrt{7}\).
Ответ: \(S_{ADC_1B_1} = 16\sqrt{7}\).
Дано правильная призма \(ABCDA_1B_1C_1D_1\). Основание призмы — квадрат. Угол между диагональю боковой грани и плоскостью основания равен \(60^\circ\), то есть \(\angle(AC_1, ABC) = 60^\circ\). Диагональ основания \(AC = 4\sqrt{2}\) см. Необходимо найти площадь четырехугольника \(S_{ADC_1B_1}\).
Сначала определим сторону квадрата основания. Диагональ квадрата выражается через его сторону \(x\) как \(AC = x\sqrt{2}\). Подставляя известное значение диагонали \(AC = 4\sqrt{2}\), получаем:
\(
x\sqrt{2} = 4\sqrt{2} \quad \Rightarrow \quad x = 4 \, \text{см}.
\)
Так как угол между диагональю боковой грани и плоскостью основания равен \(60^\circ\), то по построению \(\angle(C_1AC) = \angle(AC_1, ABC) = 60^\circ\).
Рассмотрим треугольник \(AC_1C\). В нем известно, что \(\tan(\angle C_1AC) = \frac{CC_1}{AC}\). Отсюда найдем высоту призмы \(CC_1\):
\(
CC_1 = AC \cdot \tan(\angle C_1AC) = 4\sqrt{2} \cdot \tan(60^\circ) = 4\sqrt{2} \cdot \sqrt{3} = 4\sqrt{6} \, \text{см}.
\)
Теперь рассмотрим треугольник \(AB_1B\), чтобы найти длину диагонали боковой грани \(AB_1\). В этом треугольнике \(AB_1\) является гипотенузой, а катеты \(AB\) и \(B_1B\) равны соответственно стороне основания и высоте призмы. Применяя теорему Пифагора, получаем:
\(
AB_1^2 = AB^2 + B_1B^2 = 4^2 + (4\sqrt{6})^2 = 16 + 96 = 112 \quad \Rightarrow \quad\)
\( AB_1 = \sqrt{112} (= 4\sqrt{7}.
\)
Площадь искомого четырехугольника \(ADC_1B_1\) можно найти как произведение длины диагонали \(AB_1\) на сторону основания \(AD\), так как \(AD = AB = 4\). Таким образом:
\(
S_{ADC_1B_1} = AB_1 \cdot AD = 4\sqrt{7} \cdot 4 = 16\sqrt{7} \, \text{см}^2.
\)
Ответ: \(S_{ADC_1B_1} = 16\sqrt{7} \, \text{см}^2\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!