ГДЗ по Геометрии 10 класс Номер 223 Атанасян — Подробные Ответы

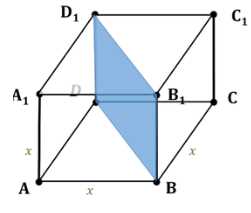
Через два противолежащих ребра куба проведено сечение, площадь которого равна \(64\sqrt{2}\) см\(^2\). Найдите ребро куба и его диагональ.

Дано: куб \(ABCDA_1B_1C_1D_1\), площадь треугольника \(S_{B_1BD_1} = 64 \cdot \sqrt{2} \, \text{см}^2\).
Найти: сторону \(x\) и диагональ \(d\).

Решение:
Площадь треугольника:
\(
S_{B_1BD_1} = \frac{1}{2} \cdot x \cdot (x \cdot \sqrt{2}) = \frac{1}{2} \cdot x^2 \cdot \sqrt{2}.
\)
Приравняем к \(64 \cdot \sqrt{2}\):
\(
\frac{1}{2} \cdot x^2 \cdot \sqrt{2} = 64 \cdot \sqrt{2}.
\)
Сократим на \(\sqrt{2}\) и умножим на 2:
\(
x^2 = 128, \quad x = \sqrt{128} = 8 \, \text{см}.
\)
Диагональ куба:
\(
d = x \cdot \sqrt{3} = 8 \cdot \sqrt{3} \, \text{см}.
\)

Ответ: сторона \(8 \, \text{см}\), диагональ \(8 \cdot \sqrt{3} \, \text{см}\).

Дано, что фигура является кубом \(ABCDA_1B_1C_1D_1\), и площадь треугольника \(S_{B_1BD_1} = 64 \cdot \sqrt{2} \, \text{см}^2\). Необходимо найти сторону куба \(x\) и его диагональ \(d\).

Обозначим сторону куба за \(x\). Заметим, что треугольник \(B_1BD_1\) является прямоугольным, так как куб имеет прямые углы. Этот треугольник образован диагоналями граней куба.

Выразим площадь треугольника \(B_1BD_1\) через стороны куба. Одна из сторон треугольника \(B_1B\) равна \(x\), другая сторона \(BD_1\) — это диагональ квадрата с длиной стороны \(x\). Диагональ квадрата равна \(x \cdot \sqrt{2}\). Таким образом, стороны треугольника равны \(x\) и \(x \cdot \sqrt{2}\).

Площадь треугольника \(B_1BD_1\) вычисляется по формуле:
\(
S_{B_1BD_1} = \frac{1}{2} \cdot B_1B \cdot BD_1 = \frac{1}{2} \cdot x \cdot (x \cdot \sqrt{2}).
\)

Упростим выражение для площади:
\(
S_{B_1BD_1} = \frac{1}{2} \cdot x^2 \cdot \sqrt{2}.
\)

По условию задачи площадь треугольника равна \(64 \cdot \sqrt{2} \, \text{см}^2\). Приравняем:
\(
\frac{1}{2} \cdot x^2 \cdot \sqrt{2} = 64 \cdot \sqrt{2}.
\)

Упростим уравнение, сократив на \(\sqrt{2}\):
\(
\frac{1}{2} \cdot x^2 = 64.
\)

Умножим обе части уравнения на 2:
\(
x^2 = 128.
\)

Найдем \(x\), извлекая квадратный корень:
\(
x = \sqrt{128} = 8.
\)

Таким образом, сторона куба равна \(x = 8 \, \text{см}\).

Теперь найдем диагональ куба \(d\). Диагональ куба проходит через весь его объем и соединяет противоположные вершины. Она вычисляется по формуле:
\(
d = x \cdot \sqrt{3}.
\)

Подставим значение \(x = 8\):
\(
d = 8 \cdot \sqrt{3}.
\)

Диагональ куба равна \(8 \cdot \sqrt{3} \, \text{см}\).