ГДЗ по Геометрии 10 класс Номер 222 Атанасян — Подробные Ответы

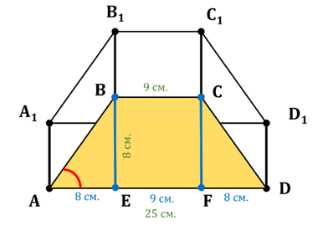
Основанием прямой призмы является равнобедренная трапеция с основаниями 25 см и 9 см и высотой 8 см. Найдите двугранные углы при боковых рёбрах призмы

Дано:
\(ABCD\) — равнобедренная трапеция, \(BC = 9 \, \text{см}\), \(AD = 25 \, \text{см}\), \(h_{ABCD} = 8 \, \text{см}\).

Найти двугранные углы при боковых ребрах призмы.

Решение:
По построению прямой призмы линейные углы искомых двугранных углов равны углам трапеции \(ABCD\).

Рассмотрим равнобедренную трапецию \(ABCD\). Построим высоты \(AE\) и \(FD\) к большему основанию.
\(
AE = BE = 8 \, \text{см}, \quad EF = AD — BC = 25 — 9 = 16 \, \text{см}
\)
Треугольник \(\triangle ABE\) прямоугольный и равнобедренный, следовательно:
\(
\angle BAE = 45^\circ
\)

Остальные углы:
\(
\angle ABC = \angle BCD = 180^\circ — 45^\circ = 135^\circ
\)

Ответ: \(45^\circ, 135^\circ, 135^\circ, 45^\circ\).

Дано: \(ABCD\) — равнобедренная трапеция, \(BC = 9 \, \text{см}\), \(AD = 25 \, \text{см}\), \(h_{ABCD} = 8 \, \text{см}\). Необходимо найти двугранные углы при боковых ребрах призмы.

Рассмотрим трапецию \(ABCD\). Согласно свойствам прямой призмы, линейные углы искомых двугранных углов совпадают с углами трапеции \(ABCD\), так как боковые ребра призмы перпендикулярны основаниям.

Построим высоты \(AE\) и \(FD\) к большему основанию \(AD\). Эти высоты разделяют трапецию \(ABCD\) на два прямоугольных треугольника (\(\triangle ABE\) и \(\triangle CDF\)) и один прямоугольник (\(BEFC\)).

Вычислим длину отрезка \(EF\), который является средней частью между высотами:
\(
EF = AD — BC = 25 — 9 = 16 \, \text{см}
\)

Теперь рассмотрим треугольник \(\triangle ABE\). Этот треугольник является прямоугольным, так как \(AE\) — высота, и равнобедренным, так как \(AE = BE = 8 \, \text{см}\). В равнобедренном прямоугольном треугольнике углы при основании равны \(45^\circ\). Следовательно:
\(
\angle BAE = 45^\circ
\)

Так как трапеция \(ABCD\) равнобедренная, угол \(\angle BAE\) равен углу \(\angle CDF\), то есть:
\(
\angle CDF = 45^\circ
\)

Теперь вычислим углы при основании \(AB\) и \(CD\). Эти углы являются внутренними односторонними углами при параллельных прямых \(BC\) и \(AD\) и секущих \(AB\) и \(CD\). Сумма таких углов равна \(180^\circ\). Учитывая, что один из углов равен \(45^\circ\), второй угол будет равен:
\(
\angle ABC = \angle BCD = 180^\circ — 45^\circ = 135^\circ
\)

Таким образом, двугранные углы при боковых ребрах призмы равны \(45^\circ, 135^\circ, 135^\circ, 45^\circ\).