ГДЗ по Геометрии 10 класс Номер 219 Атанасян — Подробные Ответы

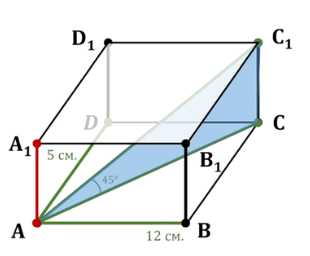
В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в \(45^\circ\). Найдите боковое ребро параллелепипеда.

Дано \(ABCD{A_1}{B_1}{C_1}{D_1}\) — прямоугольный параллелепипед. Известно, что \(AB = 12 \, \text{см}\), \(AD = 5 \, \text{см}\), \(\angle(AC_1, ABC) = 45^\circ\). Требуется найти \(AA_1\).

Сначала находим диагональ основания \(AC\) с помощью теоремы Пифагора:

\(
AC = \sqrt{AB^2 + AD^2} = \sqrt{12^2 + 5^2} = \sqrt{144 + 25} = \sqrt{169} = 13 \, \text{см}.
\)

Угол между диагональю основания \(AC\) и диагональю параллелепипеда \(AC_1\) равен \(45^\circ\). В прямоугольном треугольнике \(AC_1C\) катеты равны, так как \(\tan(45^\circ) = 1\). Следовательно:

\(
CC_1 = AC \cdot \tan(45^\circ) = 13 \cdot 1 = 13 \, \text{см}.
\)

Так как \(CC_1 = AA_1\), то \(AA_1 = 13 \, \text{см}\).

Ответ: \(AA_1 = 13 \, \text{см}\).

Дано \(ABCD{A_1}{B_1}{C_1}{D_1}\) — прямоугольный параллелепипед. Известно, что \(AB = 12 \, \text{см}\), \(AD = 5 \, \text{см}\), \(\angle(AC_1, ABC) = 45^\circ\). Необходимо найти длину \(AA_1\), то есть высоту параллелепипеда.

Для начала определим длину диагонали основания \(AC\). Основание \(ABCD\) является прямоугольником, поэтому для нахождения диагонали \(AC\) используем теорему Пифагора в треугольнике \(ABC\):

\(
AC^2 = AB^2 + BC^2
\)

Подставляем известные значения \(AB = 12 \, \text{см}\) и \(BC = AD = 5 \, \text{см}\):

\(
AC^2 = 12^2 + 5^2 = 144 + 25 = 169
\)

Извлекаем квадратный корень:

\(
AC = \sqrt{169} = 13 \, \text{см}
\)

Таким образом, длина диагонали основания \(AC\) равна \(13 \, \text{см}\).

Далее известно, что угол между диагональю основания \(AC\) и диагональю параллелепипеда \(AC_1\) равен \(45^\circ\). Это означает, что в треугольнике \(AC_1C\), который является прямоугольным, угол \(\angle C_1AC = 45^\circ\).

По свойству прямоугольного треугольника, где угол равен \(45^\circ\), катеты равны друг другу. Это значит, что высота \(AA_1\) равна длине другого катета \(CC_1\), который можно найти через тангенс угла:

\(
\tan(\angle C_1AC) = \frac{CC_1}{AC}
\)

Подставляем \(\tan(45^\circ) = 1\) и \(AC = 13 \, \text{см}\):

\(
1 = \frac{CC_1}{13} \quad \Rightarrow \quad CC_1 = 13 \cdot 1 = 13 \, \text{см}
\)

Так как \(CC_1 = AA_1\), то высота \(AA_1\) равна \(13 \, \text{см}\).

Ответ: \(AA_1 = 13 \, \text{см}\).