
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 218 Атанасян — Подробные Ответы
Докажите, что:
а) у прямой призмы все боковые грани — прямоугольники;
б) у правильной призмы все боковые грани — равные прямоугольники.
Дано: прямая призма.
Доказать:
а) у прямой призмы все боковые грани — прямоугольники,
б) у правильной прямой призмы все боковые грани — равные прямоугольники.
Решение:
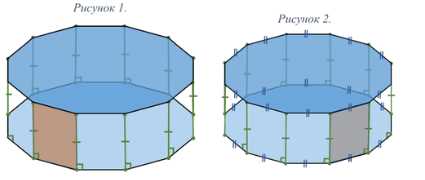
По построению каждый четырехугольник (выделен) — параллелограмм (вертикальные стороны и горизонтальные стороны параллельны).
С углом \(90^\circ\) \(\Rightarrow\) каждый выделенный четырехугольник — прямоугольник \(\Rightarrow\)
а) у прямой призмы все боковые грани — прямоугольники.
В правильной призме все стороны многоугольника равны \(\Rightarrow\) равны прямоугольники \(\Rightarrow\)
б) у правильной прямой призмы все боковые грани — равные прямоугольники.
Ответ:
а) у прямой призмы все боковые грани — прямоугольники,
б) у правильной прямой призмы все боковые грани — равные прямоугольники.
Дано: прямая призма. Необходимо доказать два утверждения. Во-первых, что у прямой призмы все боковые грани являются прямоугольниками. Во-вторых, что у правильной прямой призмы все боковые грани являются равными прямоугольниками.
Рассмотрим первое утверждение. У прямой призмы боковые грани представляют собой четырехугольники, образованные вертикальными сторонами ребер призмы и горизонтальными сторонами основания. По определению прямой призмы вертикальные стороны ребер призмы параллельны друг другу и перпендикулярны основаниям. Горизонтальные стороны основания также параллельны друг другу. Таким образом, каждый боковой четырехугольник является параллелограммом, так как противоположные его стороны параллельны.
Теперь, поскольку вертикальные ребра перпендикулярны основаниям, каждый угол между вертикальной стороной и горизонтальной стороной основания равен 90 градусам. Следовательно, боковые грани призмы, являясь параллелограммами с прямыми углами, становятся прямоугольниками. Это доказывает первое утверждение.
Рассмотрим второе утверждение. У правильной прямой призмы основание представляет собой правильный многоугольник, то есть все стороны основания равны. Поскольку боковые грани призмы образуются вертикальными ребрами и сторонами основания, а вертикальные ребра имеют одинаковую длину, каждая боковая грань будет прямоугольником, у которого одна сторона равна длине вертикального ребра, а другая сторона равна длине стороны основания.
Так как в правильной призме все стороны основания равны, все боковые грани будут равными прямоугольниками. Это доказывает второе утверждение.
Итак, в результате мы доказали, что у прямой призмы все боковые грани являются прямоугольниками, а у правильной прямой призмы все боковые грани являются равными прямоугольниками.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!