Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 217 Атанасян — Подробные Ответы
Сумма площадей трёх граней прямоугольного параллелепипеда, имеющих общую вершину, равна \(404 \, \text{дм}^2\), а его рёбра пропорциональны числам 3, 7 и 8. Найдите диагональ параллелепипеда
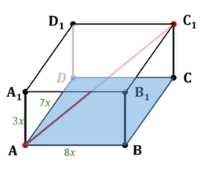
Дан прямоугольный параллелепипед с соотношением сторон \(AA_1 : AD : AB = 3 : 7 : 8\). Пусть \(x\) — коэффициент пропорциональности, тогда \(AA_1 = 3x\), \(AD = 7x\), \(AB = 8x\). Сумма площадей трёх граней равна \(404 \, \text{дм}^2\). Выразим площади: \(S_{AA_1B_1} = 24x^2\), \(S_{AA_1D_1} = 21x^2\), \(S_{ABD} = 56x^2\). Суммируем: \(101x^2 = 404\). Решая уравнение, получаем \(x^2 = 4\), значит \(x = 2\). Тогда \(AA_1 = 6 \, \text{дм}\), \(AD = 14 \, \text{дм}\), \(AB = 16 \, \text{дм}\). Для нахождения диагонали \(AC_1\) используем теорему Пифагора: сначала находим \(AC\), \(AC^2 = 16^2 + 14^2 = 452\), затем \(AC_1^2 = 452 + 6^2 = 488\). Таким образом, \(AC_1 = \sqrt{488}\).
Дан прямоугольный параллелепипед \( ABCDA_1B_1C_1D_1 \), где соотношение сторон \( AA_1 : AD : AB = 3 : 7 : 8 \). Пусть \( x \) — коэффициент пропорциональности. Тогда длины сторон можно выразить следующим образом:
\(
AA_1 = 3x, \, AD = 7x, \, AB = 8x.
\)
По условию задачи, сумма площадей трёх граней параллелепипеда равна \( 404 \, \text{дм}^2 \). Эти грани — \( S_{AA_1B_1} \), \( S_{AA_1D_1} \) и \( S_{ABD} \). Выразим их площади:
\(
S_{AA_1B_1} = AA_1 \cdot AB = 3x \cdot 8x = 24x^2,
\)
\(
S_{AA_1D_1} = AA_1 \cdot AD = 3x \cdot 7x = 21x^2,
\)
\(
S_{ABD} = AB \cdot AD = 8x \cdot 7x = 56x^2.
\)
Суммируем площади:
\(
S_{AA_1B_1} + S_{AA_1D_1} + S_{ABD} = 24x^2 + 21x^2 + 56x^2 = 101x^2.
\)
По условию задачи, эта сумма равна \( 404 \, \text{дм}^2 \). Получаем уравнение:
\(
101x^2 = 404.
\)
Решаем его:
\(
x^2 = \frac{404}{101} = 4 \quad \text{и} \quad x = 2.
\)
Теперь подставляем значение \( x \), чтобы найти длины сторон:
\(
AA_1 = 3x = 6 \, \text{дм}, \, AD = 7x = 14 \, \text{дм}, \, AB = 8x = 16 \, \text{дм}.
\)
Далее, чтобы найти диагональ \( AC_1 \), сначала вычислим диагональ основания \( AC \) в прямоугольнике \( ABC \). Применяем теорему Пифагора:
\(
AC^2 = AB^2 + BC^2.
\)
Так как \( BC = AD = 14 \, \text{дм} \), подставляем значения:
\(
AC^2 = 16^2 + 14^2 = 256 + 196 = 452.
\)
Теперь переходим к треугольнику \( ACC_1 \), в котором \( AC_1 \) — гипотенуза, а \( AC \) и \( CC_1 \) — катеты. Длина \( CC_1 \) равна \( AA_1 = 6 \, \text{дм} \). Применяем теорему Пифагора:
\(
AC_1^2 = AC^2 + CC_1^2.
\)
Подставляем значения:
\(
AC_1^2 = 452 + 6^2 = 452 + 36 = 488.
\)
Извлекаем корень:
\(
AC_1 = \sqrt{488}.
\)
Таким образом, диагональ \( AC_1 \) равна \( \sqrt{488} \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.