ГДЗ по Геометрии 10 класс Номер 216 Атанасян — Подробные Ответы

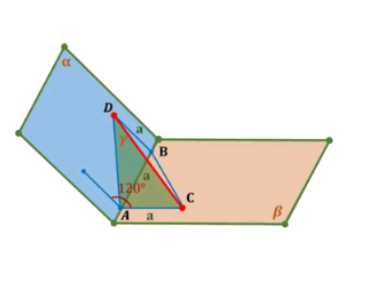
Точки \(A\) и \(B\) лежат на ребре данного двугранного угла, равного \(120^\circ\). Отрезки \(AC\) и \(BD\) проведены в разных гранях и перпендикулярны к ребру двугранного угла. Найдите отрезок \(CD\), если \(AB = AC = BD = a\)

Дано:
\( AB = AC = BD = a \),
\(\angle (\alpha, \beta) = 120^\circ\),
\( AD \perp AB \), \( CB \perp AB \).

Найти: \( CD \).

Решение:
В треугольнике \( \triangle ABD \) прямоугольный, по теореме Пифагора:
\(
AD = \sqrt{(DB)^2 + (AB)^2} = \sqrt{a^2 + a^2} = a \cdot \sqrt{2}.
\)

Угол \(\angle DAC = 120^\circ\). По теореме косинусов:
\(
DC^2 = AD^2 + AC^2 — 2 \cdot AD \cdot AC \cdot \cos (\angle DAC).
\)
Подставим значения:
\(
DC^2 = (a \cdot \sqrt{2})^2 + a^2 — 2 \cdot a \cdot \sqrt{2} \cdot a \cdot \left(-\frac{1}{2}\right).
\)
\(
DC^2 = 2a^2 + a^2 + a^2 = 4a^2.
\)
\(
DC = \sqrt{4a^2} = 2a.
\)

Ответ: \( CD = 2a \).

Дано:
\( AB = AC = BD = a \),
\(\angle (\alpha, \beta) = 120^\circ\),
\( AD \perp AB \), \( CB \perp AB \).

Найти: \( CD \).

Рассмотрим треугольник \( \triangle ABD \). Он является прямоугольным, так как \( AD \perp AB \). По теореме Пифагора для треугольника \( \triangle ABD \) находим длину гипотенузы \( AD \):
\(
AD = \sqrt{(DB)^2 + (AB)^2}.
\)
Подставляем значения \( DB = a \) и \( AB = a \):
\(
AD = \sqrt{a^2 + a^2} = \sqrt{2a^2} = a \cdot \sqrt{2}.
\)

Теперь рассмотрим треугольник \( \triangle ADC \). В этом треугольнике угол \( \angle DAC = 120^\circ \). Для нахождения \( CD \) используем теорему косинусов:
\(
DC^2 = AD^2 + AC^2 — 2 \cdot AD \cdot AC \cdot \cos(\angle DAC).
\)
Подставляем значения:
\(
DC^2 = (a \cdot \sqrt{2})^2 + a^2 — 2 \cdot (a \cdot \sqrt{2}) \cdot a \cdot \cos(120^\circ).
\)
Сначала вычислим \( \cos(120^\circ) \). Из тригонометрии известно, что \( \cos(120^\circ) = -\frac{1}{2} \). Подставляем это значение:
\(
DC^2 = (a \cdot \sqrt{2})^2 + a^2 — 2 \cdot (a \cdot \sqrt{2}) \cdot a \cdot \left(-\frac{1}{2}\right).
\)

Выполним поэтапные вычисления.
Во-первых, вычислим \( (a \cdot \sqrt{2})^2 \):
\(
(a \cdot \sqrt{2})^2 = 2a^2.
\)
Во-вторых, вычислим произведение \( -2 \cdot (a \cdot \sqrt{2}) \cdot a \cdot \left(-\frac{1}{2}\right) \):
\(
-2 \cdot a \cdot \sqrt{2} \cdot a \cdot \left(-\frac{1}{2}\right) = a^2 \cdot \sqrt{2}.
\)
Теперь подставим все в формулу:
\(
DC^2 = 2a^2 + a^2 + a^2 \cdot \sqrt{2}.
\)
Сложим однородные члены:
\(
DC^2 = 2a^2 + a^2 + a^2 = 4a^2.
\)
Найдем \( DC \), извлекая квадратный корень:
\(
DC = \sqrt{4a^2} = 2a.
\)

Ответ: \( CD = 2a \).