
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 215 Атанасян — Подробные Ответы
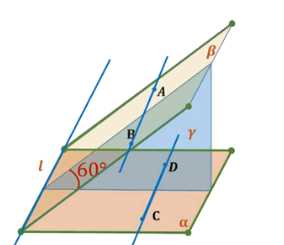
Параллельные прямые \(AB\) и \(CD\) лежат в разных гранях двугранного угла, равного \(60^\circ\). Точки \(A\) и \(D\) удалены от ребра двугранного угла соответственно на 8 см и 6,5 см. Найдите расстояние между прямыми \(AB\) и \(CD\)
Дано: \(AB \parallel CD\), \(AB \subset \beta\), \(CD \subset \alpha\), \(\alpha \cap \beta = l\), \(\angle(\alpha, \beta) = 60^\circ\), расстояние от \(AB\) до \(l = 8 \, \text{см}\), расстояние от \(CD\) до \(l = 6.5 \, \text{см}\).
Требуется найти расстояние \(EF\) между прямыми \(AB\) и \(CD\).
Решение:
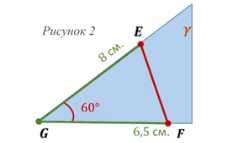
Прямые \(AB, CD, l\) параллельны. В плоскости \(y\), перпендикулярной \(AB, CD\) и \(l\), образуется треугольник \(\triangle EFG\), где:
\(
EG = 8 \, \text{см}, \, GF = 6.5 \, \text{см}, \, \angle EGF = 60^\circ.
\)
Применяем теорему косинусов:
\(
EF^2 = EG^2 + FG^2 — 2 \cdot EG \cdot FG \cdot \cos(\angle EGF).
\)
Подставляем значения:
\(
EF^2 = 8^2 + (6.5)^2 — 2 \cdot 8 \cdot 6.5 \cdot \frac{1}{2}.
\)
Вычисляем:
\(
EF^2 = 64 + 42.25 — 52 = 54.25.
\)
Следовательно:
\(
EF = \sqrt{54 \frac{1}{4}}.
\)
Ответ: \(EF = \sqrt{54 \frac{1}{4}}\).
Дано три параллельные прямые: \(AB \parallel CD \parallel l\). Прямые \(AB\) и \(CD\) лежат в разных плоскостях \(\beta\) и \(\alpha\), которые пересекаются по прямой \(l\). Угол между плоскостями \(\alpha\) и \(\beta\) равен \(60^\circ\). Расстояние от прямой \(AB\) до прямой \(l\) равно \(8 \, \text{см}\), а расстояние от прямой \(CD\) до прямой \(l\) равно \(6.5 \, \text{см}\). Требуется найти расстояние между прямыми \(AB\) и \(CD\).
Для решения задачи вводим вспомогательную плоскость \(y\), которая перпендикулярна всем трём прямым \(AB\), \(CD\) и \(l\). В этой плоскости \(y\) образуется треугольник \( \triangle EFG\), где:
— \(E\) — точка пересечения плоскости \(y\) с прямой \(AB\),
— \(F\) — точка пересечения плоскости \(y\) с прямой \(CD\),
— \(G\) — точка пересечения плоскости \(y\) с прямой \(l\).
В треугольнике \( \triangle EFG\) известно:
— \(EG = 8 \, \text{см}\) — расстояние от прямой \(AB\) до прямой \(l\),
— \(GF = 6.5 \, \text{см}\) — расстояние от прямой \(CD\) до прямой \(l\),
— \(\angle EGF = 60^\circ\) — угол между плоскостями \(\alpha\) и \(\beta\).
Для нахождения расстояния \(EF\) между прямыми \(AB\) и \(CD\) применяем теорему косинусов:
\(
EF^2 = EG^2 + GF^2 — 2 \cdot EG \cdot GF \cdot \cos(\angle EGF).
\)
Подставляем известные значения:
\(
EF^2 = 8^2 + (6.5)^2 — 2 \cdot 8 \cdot 6.5 \cdot \cos(60^\circ).
\)
Так как \(\cos(60^\circ) = \frac{1}{2}\), выражение принимает вид:
\(
EF^2 = 8^2 + (6.5)^2 — 2 \cdot 8 \cdot 6.5 \cdot \frac{1}{2}.
\)
Выполним вычисления поэтапно:
\(
8^2 = 64, \quad (6.5)^2 = 42.25, \quad 2 \cdot 8 \cdot 6.5 \cdot \frac{1}{2} = 52.
\)
Подставляем эти значения:
\(
EF^2 = 64 + 42.25 — 52.
\)
Складываем и вычитаем:
\(
EF^2 = 54.25.
\)
Находим \(EF\), извлекая корень:
\(
EF = \sqrt{54.25}.
\)
Представим \(54.25\) в виде дроби:
\(
54.25 = 54 \frac{1}{4} = \frac{217}{4}.
\)
Извлекаем корень:
\(
EF = \sqrt{\frac{217}{4}} = \frac{\sqrt{217}}{2}.
\)
Ответ:
\(
EF = \sqrt{54 \frac{1}{4}}.
\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!