ГДЗ по Геометрии 10 класс Номер 213 Атанасян — Подробные Ответы

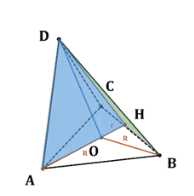
Правильные треугольники \(ABC\) и \(DBC\) расположены так, что вершина \(D\) проектируется в центр треугольника \(ABC\). Вычислите угол между плоскостями этих треугольников.

Дано: \(\triangle ABC\), \(\triangle DBC\) – правильные, \(O\) – центр треугольника \(\triangle ABC\), \(DO \perp ABC\).
Найти: \(\angle(ABC, DBC)\).

Обозначим радиус вписанной окружности правильного \(\triangle ABC\) через \(r\), а сторону \(\triangle ABC\) за \(x\).
Из курса планиметрии известно, что:
\(
r = \frac{x}{2 \cdot \sqrt{3}}
\)

Рассмотрим \(\triangle DHB\):
По теореме Пифагора:
\(
DH = \sqrt{(DB)^2 — (HB)^2} = \sqrt{x^2 — \left(\frac{x}{2}\right)^2} = x \cdot \sqrt{\frac{3}{4}}
\)

Рассмотрим \(\triangle DHO\):
\(
\cos(\angle OHD) = \frac{OH}{HD} = \frac{r}{x \cdot \sqrt{\frac{3}{4}}} = \frac{\frac{x}{2 \cdot \sqrt{3}}}{x \cdot \frac{\sqrt{3}}{2}} = \frac{1}{3}
\)

\(
\angle OHD = \arccos\left(\frac{1}{3}\right)
\)

Ответ: \(\angle OHD = \arccos\left(\frac{1}{3}\right)\).

Дано два правильных треугольника \(\triangle ABC\) и \(\triangle DBC\). Центр треугольника \(\triangle ABC\) обозначен как \(O\), а высота \(DO\) перпендикулярна плоскости треугольника \(\triangle ABC\). Требуется найти угол между плоскостями \((ABC)\) и \((DBC)\), который равен линейному углу двугранного угла \(\angle OHD\).

Обозначим сторону треугольника \(\triangle ABC\) через \(x\), а радиус вписанной окружности правильного треугольника \(\triangle ABC\) через \(r\). Из курса планиметрии известно, что радиус вписанной окружности правильного треугольника равен \(r = \frac{x}{2 \cdot \sqrt{3}}\).

Рассмотрим треугольник \(\triangle DHB\). В этом треугольнике \(DB\) – это сторона правильного треугольника \(\triangle DBC\), а \(HB\) – половина стороны правильного треугольника \(\triangle ABC\). Поэтому \(DB = x\) и \(HB = \frac{x}{2}\). По теореме Пифагора найдем длину \(DH\):
\(
DH = \sqrt{(DB)^2 — (HB)^2} = \sqrt{x^2 — \left(\frac{x}{2}\right)^2}
\)
\(
DH = \sqrt{x^2 — \frac{x^2}{4}} = \sqrt{\frac{4x^2}{4} — \frac{x^2}{4}} = \sqrt{\frac{3x^2}{4}} = x \cdot \sqrt{\frac{3}{4}}
\)

Теперь рассмотрим треугольник \(\triangle DHO\). В этом треугольнике \(OH\) – это радиус вписанной окружности треугольника \(\triangle ABC\), равный \(r = \frac{x}{2 \cdot \sqrt{3}}\), а \(HD\) уже найдено и равно \(x \cdot \sqrt{\frac{3}{4}}\). Косинус угла \(\angle OHD\) можно найти как отношение прилежащего катета \(OH\) к гипотенузе \(HD\):
\(
\cos(\angle OHD) = \frac{OH}{HD} = \frac{\frac{x}{2 \cdot \sqrt{3}}}{x \cdot \sqrt{\frac{3}{4}}}
\)
Сократим \(x\) в числителе и знаменателе:
\(
\cos(\angle OHD) = \frac{\frac{1}{2 \cdot \sqrt{3}}}{\sqrt{\frac{3}{4}}} = \frac{\frac{1}{2 \cdot \sqrt{3}}}{\frac{\sqrt{3}}{2}} = \frac{1}{3}
\)

Таким образом, угол \(\angle OHD\) равен:
\(
\angle OHD = \arccos\left(\frac{1}{3}\right)
\)

Ответ: \(\angle OHD = \arccos\left(\frac{1}{3}\right)\).