Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 212 Атанасян — Подробные Ответы
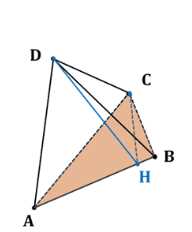
Точка \(C\) является проекцией точки \(D\) на плоскость треугольника \(ABC\). Докажите, что площадь треугольника \(ABD\) равна \(\frac{S}{\cos \alpha}\), где \(S\) — площадь треугольника \(ABC\), а \(\alpha\) — угол между плоскостями \(ABC\) и \(ABD\).
Дано: \(A \in \beta, B \in \beta, D \notin \beta\), \(C \in \beta, CD \perp \beta\), \(S_{ABC} = s\), \(\angle(ABC, ABD) = \alpha\).
Доказать: \(S_{ABD} = \frac{s}{\cos(\alpha)}\).
Решение:
Проведем высоту \(DH\) в \(\triangle ABD\). По свойству проекции и теореме о трёх перпендикулярах: \(CH \perp AB \Rightarrow CH\) — высота \(\triangle ABD\).
Рассмотрим \(\triangle DCH\):
По построению \(\angle DHC = \alpha\), так как \(\triangle DCH\) прямоугольный, \(\cos(\alpha) = \frac{CH}{DH} \Rightarrow DH = \frac{CH}{\cos(\alpha)}\).
Площадь \(\triangle ABD\):
\(
S_{ABD} = \frac{1}{2} \cdot AB \cdot DH = \frac{1}{2} \cdot AB \cdot \frac{CH}{\cos(\alpha)} = \frac{S_{ABC}}{\cos(\alpha)} = \frac{s}{\cos(\alpha)}.
\)
Что и требовалось доказать.
Ответ: \(S_{ABD} = \frac{s}{\cos(\alpha)}\).
Дано, что точки \(A\), \(B\) и \(C\) лежат в плоскости \(\beta\), а точка \(D\) не принадлежит этой плоскости. Прямая \(CD\) перпендикулярна плоскости \(\beta\), площадь треугольника \(ABC\) обозначена как \(s\), угол между плоскостями \((ABC)\) и \((ABD)\) равен \(\alpha\). Необходимо доказать, что площадь треугольника \(ABD\) равна \(\frac{s}{\cos(\alpha)}\).
Для нахождения площади треугольника \(ABD\) проведем высоту \(DH\) из точки \(D\) к плоскости треугольника \(ABD\). По свойству проекции и теореме о трех перпендикулярах высота \(CH\) треугольника \(ABC\) перпендикулярна стороне \(AB\), а также перпендикулярна плоскости треугольника \(ABD\). Следовательно, отрезок \(CH\) также является высотой треугольника \(ABD\).
Рассмотрим прямоугольный треугольник \(DCH\). Угол \(\angle DHC\) равен \(\alpha\), так как он является линейным углом двугранного угла между плоскостями \((ABC)\) и \((ABD)\). В этом треугольнике по определению косинуса имеем \(\cos(\alpha) = \frac{CH}{DH}\). Отсюда высота \(DH\) выражается как \(DH = \frac{CH}{\cos(\alpha)}\).
Площадь треугольника \(ABD\) вычисляется по формуле \(\frac{1}{2} \cdot AB \cdot DH\), где \(AB\) — сторона треугольника, а \(DH\) — высота, проведенная к этой стороне. Подставим выражение для \(DH\):
\(
S_{ABD} = \frac{1}{2} \cdot AB \cdot \frac{CH}{\cos(\alpha)}.
\)
Площадь треугольника \(ABC\) равна \(\frac{1}{2} \cdot AB \cdot CH\), то есть \(S_{ABC} = s\). Следовательно, \(CH = \frac{2s}{AB}\). Подставим это значение в формулу для \(S_{ABD}\):
\(
S_{ABD} = \frac{1}{2} \cdot AB \cdot \frac{\frac{2s}{AB}}{\cos(\alpha)}.
\)
Сократим \(AB\):
\(
S_{ABD} = \frac{s}{\cos(\alpha)}.
\)
Таким образом, площадь треугольника \(ABD\) равна \(\frac{s}{\cos(\alpha)}\), что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.