ГДЗ по Геометрии 10 класс Номер 209 Атанасян — Подробные Ответы

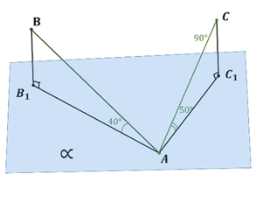
Углы между равными отрезками \(AB\) и \(AC\) и плоскостью \(\alpha\), проходящей через точку \(A\), равны соответственно \(40^\circ\) и \(50^\circ\). Сравните расстояния от точек \(B\) и \(C\) до плоскости \(\alpha\).е \(KL\) и \(KM\), образующие между собой прямой угол, а с плоскостью \(\alpha\) — углы в \(45^\circ\) и \(30^\circ\) соответственно. Найдите отрезок \(LM\).

Рассмотрим прямоугольные треугольники \(\triangle BAB_1\) и \(\triangle CAC_1\).

Из треугольника \(\triangle BAB_1\):
\(\sin(\angle BAB_1) = \frac{BB_1}{AB} \Rightarrow BB_1 = AB \cdot \sin(40^\circ)\).

Из треугольника \(\triangle CAC_1\):
\(\sin(\angle CAC_1) = \frac{CC_1}{AC} \Rightarrow CC_1 = AC \cdot \sin(50^\circ)\).

Так как \(AB = AC\):
\(\frac{BB_1}{CC_1} = \frac{AB \cdot \sin(40^\circ)}{AC \cdot \sin(50^\circ)} = \frac{\sin(40^\circ)}{\sin(50^\circ)} < 1 \Rightarrow BB_1 < CC_1\). Ответ: расстояние от точки \(B\) меньше.

Дано, что точки \(A\), \(B\), \(C\), \(B_1\), \(C_1\) лежат в плоскости \(\alpha\), причём \(BB_1 \perp \alpha\) и \(CC_1 \perp \alpha\). Также известно, что углы \(\angle BAB_1 = 40^\circ\) и \(\angle CAC_1 = 50^\circ\), а отрезки \(AB\) и \(AC\) равны (\(AB = AC\)).

Необходимо сравнить длины \(BB_1\) и \(CC_1\).

Для решения задачи сначала рассмотрим прямоугольный треугольник \(\triangle BAB_1\). В этом треугольнике один из углов равен \(40^\circ\), гипотенуза равна \(AB\), а катет \(BB_1\) перпендикулярен плоскости \(\alpha\). Используем определение синуса:
\(\sin(\angle BAB_1) = \frac{BB_1}{AB}\).
Отсюда выражаем \(BB_1\):
\(BB_1 = AB \cdot \sin(40^\circ)\).

Далее рассмотрим прямоугольный треугольник \(\triangle CAC_1\). В этом треугольнике один из углов равен \(50^\circ\), гипотенуза равна \(AC\), а катет \(CC_1\) также перпендикулярен плоскости \(\alpha\). По аналогии используем определение синуса:
\(\sin(\angle CAC_1) = \frac{CC_1}{AC}\).
Выразим \(CC_1\):
\(CC_1 = AC \cdot \sin(50^\circ)\).

Так как по условию \(AB = AC\), подставляем это равенство в полученные выражения для \(BB_1\) и \(CC_1\):
\(BB_1 = AB \cdot \sin(40^\circ)\),
\(CC_1 = AB \cdot \sin(50^\circ)\).

Теперь сравним \(BB_1\) и \(CC_1\), вычислив их отношение:
\(\frac{BB_1}{CC_1} = \frac{AB \cdot \sin(40^\circ)}{AB \cdot \sin(50^\circ)} = \frac{\sin(40^\circ)}{\sin(50^\circ)}\).

Значение \(\frac{\sin(40^\circ)}{\sin(50^\circ)}\) меньше единицы, так как \(\sin(40^\circ) < \sin(50^\circ)\). Отсюда следует, что \(BB_1 < CC_1\). Таким образом, расстояние от точки \(B\) до плоскости \(\alpha\) меньше, чем расстояние от точки \(C\) до плоскости \(\alpha\).