
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 208 Атанасян — Подробные Ответы
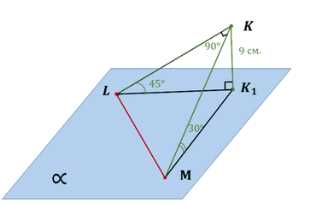
Из точки \(K\), удалённой от плоскости \(\alpha\) на 9 см, проведены к плоскости и наклонные \(KL\) и \(KM\), образующие между собой прямой угол, а с плоскостью \(\alpha\) — углы в \(45^\circ\) и \(30^\circ\) соответственно. Найдите отрезок \(LM\).
Дано: \(L \in \alpha, M \in \alpha, K \notin \alpha, K_1 \in \alpha\), \(\angle LKM = 90^\circ\), \(KK_1 \perp \alpha\), \(\angle KLK_1 = 45^\circ\), \(\angle LKMK_1 = 30^\circ\).
Из \(\triangle KLK_1\): \(\sin(\angle KLK_1) = \frac{KK_1}{KL} \Rightarrow KL = \frac{KK_1}{\sin(45^\circ)} = 9 \cdot \sqrt{2} \, \text{см}\).
Из \(\triangle KMK_1\): \(\sin(\angle LKMK_1) = \frac{KK_1}{KM} \Rightarrow KM = \frac{KK_1}{\sin(30^\circ)} = 18 \, \text{см}\).
По теореме Пифагора из \(\triangle LKM\):
\(
LM = \sqrt{(KL)^2 + (ML)^2} = \sqrt{(9 \cdot \sqrt{2})^2 + 18^2} = \sqrt{162 + 324} = \sqrt{486} = \)
\(=9 \cdot \sqrt{2} \, \text{см}.
\)
Ответ: \(LM = 9 \cdot \sqrt{2} \, \text{см}\).
Дано: \( \angle LKM = 90^\circ \), \( KK_1 \perp \alpha \), \( \angle LKK_1 = 45^\circ \), \( \angle LMK_1 = 30^\circ \), \( KK_1 = 9 \, \text{см} \). Необходимо найти \( LM \).
Для решения задачи строим проекцию точки \( K_1 \) на плоскость \( \alpha \). Из условия задачи получаем три прямоугольных треугольника: \( \triangle LKM \), \( \triangle KLK_1 \), \( \triangle KMK_1 \). Решение состоит из последовательного нахождения сторон \( KL \), \( KM \), а затем вычисления гипотенузы \( LM \) в треугольнике \( \triangle LKM \) с помощью теоремы Пифагора.
Сначала рассмотрим треугольник \( \triangle KLK_1 \). В этом треугольнике угол \( \angle LKK_1 = 45^\circ \), гипотенуза \( KK_1 = 9 \, \text{см} \), а катет \( KL \) нужно найти. Используем определение синуса:
\(
\sin(\angle LKK_1) = \frac{KK_1}{KL}.
\)
Подставляем известные значения:
\(
\sin(45^\circ) = \frac{KK_1}{KL}.
\)
Так как \( \sin(45^\circ) = \frac{\sqrt{2}}{2} \), то:
\(
\frac{\sqrt{2}}{2} = \frac{9}{KL}.
\)
Решаем это уравнение относительно \( KL \):
\(
KL = \frac{9}{\frac{\sqrt{2}}{2}} = 9 \cdot \frac{2}{\sqrt{2}} = 9 \cdot \sqrt{2} \, \text{см}.
\)
Теперь рассмотрим треугольник \( \triangle KMK_1 \). В этом треугольнике угол \( \angle LMK_1 = 30^\circ \), гипотенуза \( KK_1 = 9 \, \text{см} \), а катет \( KM \) нужно найти. Используем определение синуса:
\(
\sin(\angle LMK_1) = \frac{KK_1}{KM}.
\)
Подставляем известные значения:
\(
\sin(30^\circ) = \frac{KK_1}{KM}.
\)
Так как \( \sin(30^\circ) = \frac{1}{2} \), то:
\(
\frac{1}{2} = \frac{9}{KM}.
\)
Решаем это уравнение относительно \( KM \):
\(
KM = \frac{9}{\frac{1}{2}} = 9 \cdot 2 = 18 \, \text{см}.
\)
Теперь в прямоугольном треугольнике \( \triangle LKM \) известны катеты \( KL = 9 \cdot \sqrt{2} \, \text{см} \) и \( KM = 18 \, \text{см} \). Используем теорему Пифагора для нахождения гипотенузы \( LM \):
\(
LM = \sqrt{KL^2 + KM^2}.
\)
Подставляем значения \( KL \) и \( KM \):
\(
LM = \sqrt{(9 \cdot \sqrt{2})^2 + 18^2}.
\)
Вычислим квадраты:
\(
(9 \cdot \sqrt{2})^2 = 81 \cdot 2 = 162, \quad 18^2 = 324.
\)
Складываем:
\(
LM = \sqrt{162 + 324} = \sqrt{486}.
\)
Представим \( 486 \) как произведение:
\(
486 = 81 \cdot 6.
\)
Извлекаем корень:
\(
LM = \sqrt{81 \cdot 6} = \sqrt{81} \cdot \sqrt{6} = 9 \cdot \sqrt{6}.
\)
Ответ: \( LM = 9 \cdot \sqrt{2} \, \text{см} \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!