ГДЗ по Геометрии 10 класс Номер 207 Атанасян — Подробные Ответы

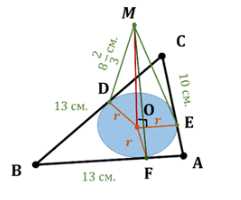
В треугольнике \(ABC\) дано: \(AB = BC = 13 \, \text{см}\), \(AC = 10 \, \text{см}\). Точка \(M\) удалена от прямых \(AB\), \(BC\) и \(AC\) на \(8 \frac{2}{3} \, \text{см}\). Найдите расстояние от точки \(M\) до плоскости \(ABC\), если её проекция на эту плоскость лежит внутри треугольника.

Дано:
\(\triangle ABC\), \(MO \perp ABC\), \(MD = ME = MF = \frac{8}{3} \, \text{см}\),
\(AB = BC = 13 \, \text{см}\), \(AC = 10 \, \text{см}\).

Найти: \(MO\).

Решение:

Построим точку \(O\).
Из построения: \(\triangle MOD = \triangle MOE = \triangle MOF\), так как \(MO\) — общий катет при равных гипотенузах. Следовательно, \(DO = EO = FO\).
По теореме о трёх перпендикулярах: \(OD \perp BC\), \(OE \perp AC\), \(OF \perp AB\).
Точка \(O\) — центр вписанной окружности.

Радиус вписанной окружности:
\(
r = \frac{\sqrt{(p — a)(p — b)(p — c)}}{p}, \quad p = \frac{AB + BC + AC}{2} = \frac{13 + 13 + 10}{2} = 18.
\)
\(
r = \frac{\sqrt{(18 — 13)(18 — 13)(18 — 10)}}{18} = \frac{\sqrt{5 \cdot 5 \cdot 8}}{18} = \frac{\sqrt{200}}{18} = \frac{10}{9} \, \text{см}.
\)

По теореме Пифагора:
\(
MO = \sqrt{(MD)^2 + (OD)^2}, \quad MD = \frac{8}{3}, \quad OD = r = \frac{10}{9}.
\)
\(
MO = \sqrt{\left(\frac{8}{3}\right)^2 + \left(\frac{10}{9}\right)^2} = \sqrt{\frac{64}{9} + \frac{100}{81}} = \sqrt{\frac{576}{81} + \frac{100}{81}} = \sqrt{\frac{676}{81}} = \frac{26}{9} \cdot 3 =\)
\(= 8 \, \text{см}.
\)

Ответ: \(MO = 8 \, \text{см}\).

Дано, что точка \(M\) находится вне плоскости треугольника \(\triangle ABC\), а прямая \(MO\) перпендикулярна плоскости \(\triangle ABC\). Также известно, что \(MD = ME = MF = \frac{8}{3}\), где \(D\), \(E\), \(F\) — точки пересечения прямых, проведённых из \(M\), с прямыми \(BC\), \(AC\), \(AB\) соответственно. Стороны треугольника заданы: \(AB = BC = 13\), \(AC = 10\). Требуется найти длину отрезка \(MO\), где \(O\) — проекция точки \(M\) на плоскость \(\triangle ABC\).

Для решения задачи сначала строим точку \(O\). Заметим, что треугольники \(\triangle MOD\), \(\triangle MOE\), \(\triangle MOF\) равны, так как у них общий катет \(MO\) и равные гипотенузы \(MD = ME = MF\). Следовательно, \(DO = EO = FO\). Это означает, что точка \(O\) является центром вписанной окружности треугольника \(\triangle ABC\).

Далее используем формулу радиуса \(r\) вписанной окружности:
\(
r = \frac{\sqrt{(p — a)(p — b)(p — c)}}{p}
\)
где \(p\) — полупериметр треугольника, \(a = BC = 13\), \(b = AB = 13\), \(c = AC = 10\). Сначала вычислим \(p\):
\(
p = \frac{a + b + c}{2} = \frac{13 + 13 + 10}{2} = 18
\)
Теперь подставим значения в формулу для радиуса:
\(
r = \frac{\sqrt{(18 — 13)(18 — 13)(18 — 10)}}{18} = \frac{\sqrt{5 \cdot 5 \cdot 8}}{18} = \frac{\sqrt{200}}{18} = \frac{10}{9} \, \text{см}
\)

Далее найдём длину \(MO\) с использованием теоремы Пифагора в треугольнике \(\triangle MOD\). Известно, что \(MD = \frac{8}{3}\), а \(OD = r = \frac{10}{9}\). Тогда:
\(
MO = \sqrt{(MD)^2 + (OD)^2}
\)
Подставим значения:
\(
MO = \sqrt{\left(\frac{8}{3}\right)^2 + \left(\frac{10}{9}\right)^2} = \sqrt{\frac{64}{9} + \frac{100}{81}}
\)
Приведём к общему знаменателю:
\(
MO = \sqrt{\frac{576}{81} + \frac{100}{81}} = \sqrt{\frac{676}{81}}
\)
Извлекаем корень:
\(
MO = \frac{\sqrt{676}}{9} = \frac{26}{9} \cdot 3 = 8 \, \text{см}
\)

Таким образом, длина отрезка \(MO\) равна \(8 \, \text{см}\).