
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 206 Атанасян — Подробные Ответы
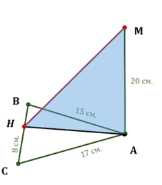
Стороны треугольника равны 17 см, 15 см и 8 см. Через вершину \(A\) меньшего угла треугольника проведена прямая \(AM\), перпендикулярная к его плоскости. Определите расстояние от точки \(M\) до прямой, содержащей меньшую сторону треугольника, если известно, что \(AM = 20 \, \text{см}\).
Дано: \(\triangle ABC\), \(AM \perp BC\), \(AC = 17 \, \text{см}\), \(AB = 15 \, \text{см}\), \(BC = 8 \, \text{см}\), \(AM = 20 \, \text{см}\). Найти: \(MH\).
Для решения задачи опускаем перпендикуляр \(AH\) на сторону \(BC\). По теореме о трёх перпендикулярах \(AH\) — это высота \(\triangle ABC\).
Площадь треугольника вычисляем по формуле Герона:
\(
S_{\triangle ABC} = \sqrt{p \cdot (p — a) \cdot (p — b) \cdot (p — c)},
\)
где \(p = \frac{a + b + c}{2}\).
Подставляем:
\(
p = \frac{17 + 15 + 8}{2} = 20 \, \text{см}.
\)
\(
S_{\triangle ABC} = \sqrt{20 \cdot (20 — 17) \cdot (20 — 15) \cdot (20 — 8)} = \sqrt{20 \cdot 3 \cdot 5 \cdot 12} = \)
\(=\sqrt{3600} = 60 \, \text{см}^2.
\)
Высота \(AH\) найдётся по формуле:
\(
AH = \frac{2 \cdot S_{\triangle ABC}}{BC} = \frac{2 \cdot 60}{8} = 15 \, \text{см}.
\)
Из прямоугольного треугольника \(\triangle AMH\) находим \(MH\) по теореме Пифагора:
\(
MH = \sqrt{AM^2 — AH^2} = \sqrt{20^2 — 15^2} = \sqrt{400 — 225} = \sqrt{175} = 25 \, \text{см}.
\)
Ответ: \(MH = 25 \, \text{см}\).
Дано: треугольник \( \triangle ABC \), в котором \( AM \perp BC \), \( AC = 17 \, \text{см} \), \( AB = 15 \, \text{см} \), \( BC = 8 \, \text{см} \), \( AM = 20 \, \text{см} \). Необходимо найти длину отрезка \( MH \).
Сначала определим площадь треугольника \( \triangle ABC \). Для этого используем формулу Герона:
\( S_{\triangle ABC} = \sqrt{p \cdot (p — a) \cdot (p — b) \cdot (p — c)} \),
где \( p \) — полупериметр треугольника, а \( a, b, c \) — длины сторон треугольника.
Вычислим полупериметр \( p \):
\( p = \frac{AB + AC + BC}{2} = \frac{15 + 17 + 8}{2} = 20 \, \text{см} \).
Теперь подставим значения сторон в формулу Герона:
\( S_{\triangle ABC} = \sqrt{20 \cdot (20 — 15) \cdot (20 — 17) \cdot (20 — 8)} \).
Выполним вычитания:
\( S_{\triangle ABC} = \sqrt{20 \cdot 5 \cdot 3 \cdot 12} \).
Упростим выражение под корнем:
\( S_{\triangle ABC} = \sqrt{3600} = 60 \, \text{см}^2 \).
Далее используем формулу площади треугольника через основание и высоту:
\( S_{\triangle ABC} = \frac{1}{2} \cdot BC \cdot AH \).
Выразим высоту \( AH \):
\( AH = \frac{2 \cdot S_{\triangle ABC}}{BC} \).
Подставим известные значения:
\( AH = \frac{2 \cdot 60}{8} = 15 \, \text{см} \).
Теперь рассмотрим прямоугольный треугольник \( \triangle AMH \), в котором \( AM \) — гипотенуза, \( AH \) — один из катетов, а \( MH \) — второй катет.
По теореме Пифагора:
\( AM^2 = AH^2 + MH^2 \).
Выразим \( MH \):
\( MH = \sqrt{AM^2 — AH^2} \).
Подставим значения:
\( MH = \sqrt{20^2 — 15^2} = \sqrt{400 — 225} = \sqrt{175} = 25 \, \text{см} \).
Ответ: \( MH = 25 \, \text{см} \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!