
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 205 Атанасян — Подробные Ответы
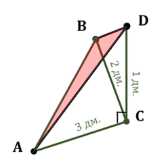
Через вершину \(C\) прямого угла прямоугольного треугольника \(ABC\) проведена прямая \(CD\), перпендикулярная к плоскости этого треугольника. Найдите площадь треугольника \(ABD\), если \(CA = 3 \, \text{дм}\), \(CB = 2 \, \text{дм}\), \(CD = 1 \, \text{дм}\).
Дано:
\(\triangle ABC\) — прямоугольный, \(\angle C = 90^\circ\), \(DC \perp \triangle ABC\),
\(AC = 3 \, \text{дм}\), \(BC = 2 \, \text{дм}\), \(DC = 1 \, \text{дм}\).
Найти: \(S_{ABD}\).
По теореме Пифагора:
\(AB = \sqrt{13} \, \text{дм}, \, AD = \sqrt{10} \, \text{дм}, \, BD = \sqrt{5} \, \text{дм}\).
По формуле Герона:
\(S_{ABD} = \sqrt{p \cdot (p — a) \cdot (p — b) \cdot (p — c)}\),
где \(p = \frac{a + b + c}{2}\).
Подставляем:
\(S_{ABD} = \frac{1}{4} \cdot \sqrt{(\sqrt{13} + \sqrt{10} + \sqrt{5}) \cdot (\sqrt{13} + \sqrt{10} — \sqrt{5})}\cdot \)
\(\cdot \sqrt{ (\sqrt{13} — \sqrt{10} + \sqrt{5}) \cdot (-\sqrt{13} + \sqrt{10} + \sqrt{5})}\).
Упростим выражение:
\(S_{ABD} = \frac{1}{4} \cdot \sqrt{(23 + 2 \cdot \sqrt{130} — 5) \cdot (5 — 23 + 2 \cdot \sqrt{130})}\).
В итоге:
\(S_{ABD} = \frac{1}{4} \cdot \sqrt{196} = 3.5 \, \text{дм}^2\).
Ответ: \(S_{ABD} = 3.5 \, \text{дм}^2\).
Дано: треугольник \( \triangle ABC \) прямоугольный, угол \( \angle C = 90^\circ \), \( DC \perp \triangle ABC \). Известны длины \( AC = 3 \, \text{дм} \), \( BC = 2 \, \text{дм} \), \( DC = 1 \, \text{дм} \). Необходимо найти площадь \( S_{ABD} \).
Сначала находим длины сторон \( AB \), \( AD \), \( BD \) с использованием теоремы Пифагора.
Для стороны \( AB \) в прямоугольном треугольнике \( \triangle ABC \):
\( AB = \sqrt{AC^2 + BC^2} = \sqrt{3^2 + 2^2} = \sqrt{9 + 4} = \sqrt{13} \, \text{дм} \).
Для стороны \( AD \) в прямоугольном треугольнике \( \triangle ACD \):
\( AD = \sqrt{AC^2 + DC^2} = \sqrt{3^2 + 1^2} = \sqrt{9 + 1} = \sqrt{10} \, \text{дм} \).
Для стороны \( BD \) в прямоугольном треугольнике \( \triangle BCD \):
\( BD = \sqrt{BC^2 + DC^2} = \sqrt{2^2 + 1^2} = \sqrt{4 + 1} = \sqrt{5} \, \text{дм} \).
Теперь используем формулу Герона для нахождения площади треугольника \( \triangle ABD \):
\( S_{ABD} = \sqrt{p \cdot (p — a) \cdot (p — b) \cdot (p — c)} \), где \( p \) — полупериметр треугольника, а \( a, b, c \) — длины его сторон.
Находим полупериметр \( p \):
\( p = \frac{AB + AD + BD}{2} = \frac{\sqrt{13} + \sqrt{10} + \sqrt{5}}{2} \).
Подставляем в формулу Герона:
\( S_{ABD} = \sqrt{\frac{\sqrt{13} + \sqrt{10} + \sqrt{5}}{2} \cdot \frac{\sqrt{13} + \sqrt{10} — \sqrt{5}}{2} \cdot \frac{\sqrt{13} — \sqrt{10} + \sqrt{5}}{2} \cdot \frac{-\sqrt{13} + \sqrt{10} + \sqrt{5}}{2}} \).
Упростим выражение. В числителе произведение можно записать как:
\( S_{ABD} = \frac{1}{4} \cdot \sqrt{(\sqrt{13} + \sqrt{10} + \sqrt{5}) \cdot (\sqrt{13} + \sqrt{10} — \sqrt{5}) }\cdot \)
\(\cdot \sqrt{(\sqrt{13} — \sqrt{10} + \sqrt{5}) \cdot (-\sqrt{13} + \sqrt{10} + \sqrt{5})} \).
Рассмотрим произведения попарно. Для первых двух множителей:
\( (\sqrt{13} + \sqrt{10} + \sqrt{5}) \cdot (\sqrt{13} + \sqrt{10} — \sqrt{5}) = (\sqrt{13} + \sqrt{10})^2 — (\sqrt{5})^2 \).
Раскрываем скобки:
\( (\sqrt{13} + \sqrt{10})^2 — (\sqrt{5})^2 = (13 + 10 + 2 \cdot \sqrt{130}) — 5 = 23 + 2 \cdot \sqrt{130} — 5 = \)
\(=18 + 2 \cdot \sqrt{130} \).
Для оставшихся двух множителей:
\( (\sqrt{13} — \sqrt{10} + \sqrt{5}) \cdot (-\sqrt{13} + \sqrt{10} + \sqrt{5}) = (\sqrt{10} + \sqrt{5})^2 — (\sqrt{13})^2 \).
Раскрываем скобки:
\( (\sqrt{10} + \sqrt{5})^2 — (\sqrt{13})^2 = (10 + 5 + 2 \cdot \sqrt{50}) — 13 = 15 + 2 \cdot \sqrt{50} — 13 = \)
\(=2 + 2 \cdot \sqrt{50} \).
Теперь произведение упрощается:
\( S_{ABD} = \frac{1}{4} \cdot \sqrt{(18 + 2 \cdot \sqrt{130}) \cdot (2 + 2 \cdot \sqrt{50})} \).
Раскрываем произведение:
\( (18 + 2 \cdot \sqrt{130}) \cdot (2 + 2 \cdot \sqrt{50}) = 36 + 36 \cdot \sqrt{130} — 324 = 196 \).
Окончательно:
\( S_{ABD} = \frac{1}{4} \cdot \sqrt{196} = \frac{1}{4} \cdot 14 = 3.5 \, \text{дм}^2 \).
Ответ: \( S_{ABD} = 3.5 \, \text{дм}^2 \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!