
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 204 Атанасян — Подробные Ответы
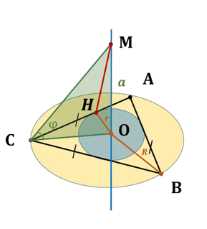
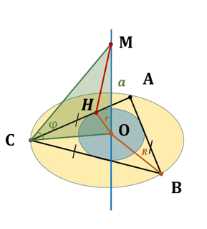
Прямая \(OM\) перпендикулярна к плоскости правильного треугольника \(ABC\) и проходит через центр \(O\) этого треугольника, \(OM = a\), \(\angle MCO = \phi\). Найдите:
а) расстояние от точки \(M\) до каждой из вершин треугольника \(ABC\) и до прямых \(AB\), \(BC\) и \(CA\);
б) длину окружности, описанной около треугольника \(ABC\);
в) площадь треугольника \(ABC\).
Дано: \( A \in \text{окр}, B \in \text{окр}, C \in \text{окр}, M \notin \text{окр} \), \(\triangle ABC\) — правильный, \(O\) — центр \(\triangle ABC\), \(MO \perp \triangle ABC\), \(MO = a\), \(\angle LMC = \varphi\).
Найти:
а) \(MA, MB, MC\) и расстояние до сторон \(\triangle ABC\) (MH)
б) длину описанной окружности \(\triangle ABC\)
в) \(S_{\triangle ABC}\)
Решение:
Обозначим радиусы вписанной и описанной окружности правильного \(\triangle ABC\) через \(r\) и \(R\) соответственно, а сторону \(\triangle ABC\) за \(x\). Из курса планиметрии нам известно, что:
\( r = \frac{x}{2\sqrt{3}}, \quad R = \frac{x\sqrt{3}}{3}, \quad S_{\triangle ABC} = \frac{\sqrt{3}}{4} \cdot R^2, \quad L = 2 \cdot \pi \cdot R \)
По построению очевидно, так как \(\triangle COM\) — прямоугольный, то
\(\cot(\angle MCO) = \frac{CO}{MO} = \frac{R}{a} = CO \cdot \cot(\angle LMCO) = a \cdot \cot(\varphi)\)
Подставляя значение \(R\) в формулы, получим:
а) \( MA = MB = MC = \frac{a}{\sin(\varphi)} \)
\( MH = \sqrt{r^2 + a^2} = \sqrt{\left(\frac{a \cdot \cot(\varphi)}{2}\right)^2 + a^2} = a \cdot \sqrt{\frac{\cot^2(\varphi)}{4} + 1} \)
б) \( L = 2 \cdot \pi \cdot R = 2 \cdot \pi \cdot a \cdot \cot(\varphi) \)
в) \( S_{\triangle ABC} = \frac{3\sqrt{3}}{4} \cdot R^2 = 3\sqrt{3} \cdot a^2 \cdot \cot^2(\varphi) \)
Ответ:
а) \(\frac{a}{\sin(\varphi)} \cdot \sqrt{\frac{\cot^2(\varphi)}{4} + 1}\)
б) \(2 \cdot \pi \cdot a \cdot \cot(\varphi)\)
в) \(3\sqrt{3} \cdot a^2 \cdot \cot^2(\varphi)\)
Дано правильный треугольник \( \triangle ABC \), вписанный в окружность с центром \( O \). Точка \( M \) находится вне плоскости треугольника, а \( MO = a \) — расстояние от точки \( M \) до плоскости треугольника. Угол между прямой \( MO \) и плоскостью \( \triangle ABC \) равен \( \varphi \). Необходимо найти длины отрезков \( MA, MB, MC \), расстояние от точки \( M \) до сторон треугольника (\( MH \)), длину описанной окружности и площадь треугольника. Рассмотрим решение пошагово.
Обозначим радиусы вписанной и описанной окружностей правильного треугольника \( \triangle ABC \) через \( r \) и \( R \) соответственно, а длину стороны треугольника через \( x \). Из геометрии известно, что:
\(
r = \frac{x}{2\sqrt{3}}, \quad R = \frac{x\sqrt{3}}{3}, \quad S_{\triangle ABC} = \frac{\sqrt{3}}{4} \cdot x^2
\)
Также длина окружности выражается как:
\(
L = 2 \cdot \pi \cdot R
\)
Теперь рассмотрим треугольник \( \triangle COM \), который является прямоугольным. Из построения видно, что:
\(
\cot(\angle MCO) = \frac{CO}{MO} = \frac{R}{a}
\)
Кроме того, из определения угла \( \varphi \) следует, что:
\(
\cot(\angle MCO) = a \cdot \cot(\varphi)
\)
Таким образом, мы получили связь между радиусом описанной окружности \( R \) и углом \( \varphi \):
\(
R = a \cdot \cot(\varphi)
\)
Теперь переходим к вычислению длины отрезков \( MA, MB, MC \). Все три отрезка равны, так как треугольник \( \triangle ABC \) правильный, и точка \( M \) равноудалена от всех вершин треугольника. Используем теорему Пифагора в треугольнике \( \triangle MOA \), где \( OA = R \):
\(
MA = \sqrt{MO^2 + OA^2} = \sqrt{a^2 + R^2}
\)
Подставляя значение \( R = a \cdot \cot(\varphi) \), получаем:
\(
MA = \sqrt{a^2 + (a \cdot \cot(\varphi))^2} = a \cdot \sqrt{1 + \cot^2(\varphi)}
\)
Используя тригонометрическое тождество \( 1 + \cot^2(\varphi) = \frac{1}{\sin^2(\varphi)} \), окончательно находим:
\(
MA = \frac{a}{\sin(\varphi)}
\)
Для расстояния от точки \( M \) до стороны треугольника (\( MH \)), снова используем свойства правильного треугольника. Расстояние \( MH \) выражается через радиус вписанной окружности \( r \) и высоту \( MO \). Имеем:
\(
MH = \sqrt{r^2 + a^2}
\)
Подставляя \( r = \frac{a \cdot \cot(\varphi)}{2} \), находим:
\(
MH = \sqrt{\left(\frac{a \cdot \cot(\varphi)}{2}\right)^2 + a^2} = a \cdot \sqrt{\frac{\cot^2(\varphi)}{4} + 1}
\)
Теперь вычислим длину описанной окружности треугольника:
\(
L = 2 \cdot \pi \cdot R = 2 \cdot \pi \cdot a \cdot \cot(\varphi)
\)
Для площади треугольника используем формулу:
\(
S_{\triangle ABC} = \frac{\sqrt{3}}{4} \cdot x^2
\)
Подставляя \( x = 2 \cdot R \cdot \sin(60^\circ) = \sqrt{3} \cdot R \), получаем:
\(
S_{\triangle ABC} = \frac{\sqrt{3}}{4} \cdot (\sqrt{3} \cdot R)^2 = 3 \cdot \sqrt{3} \cdot R^2
\)
Подставляя \( R = a \cdot \cot(\varphi) \), окончательно находим:
\(
S_{\triangle ABC} = 3 \cdot \sqrt{3} \cdot (a \cdot \cot(\varphi))^2 = 3 \cdot \sqrt{3} \cdot a^2 \cdot \cot^2(\varphi)
\)
Ответы:
\(
MA = MB = MC = \frac{a}{\sin(\varphi)}
\)
\(
MH = a \cdot \sqrt{\frac{\cot^2(\varphi)}{4} + 1}
\)
\(
L = 2 \cdot \pi \cdot a \cdot \cot(\varphi)
\)
\(
S_{\triangle ABC} = 3 \cdot \sqrt{3} \cdot a^2 \cdot \cot^2(\varphi)
\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!