ГДЗ по Геометрии 10 класс Номер 202 Атанасян — Подробные Ответы

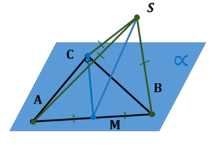
Точка удалена от каждой из вершин прямоугольного треугольника на расстояние 10 см. На каком расстоянии от плоскости треугольника находится эта точка, если медиана, проведённая к гипотенузе, равна 5 см?

Дано: \(\triangle ABC\) — прямоугольный (\(\angle C = 90^\circ\)), \(SA = SB = SC = 10\) см, \(CM = 5\) см.
Доказать: \(SM \perp \alpha\).

Решение:

По построению \(\triangle ASB\) равнобедренный, поэтому медиана, проведённая к основанию, является высотой: \(SM \perp AB\).

По свойству прямоугольного треугольника, медиана, проведённая к гипотенузе, равна её половине: \(CM = AM = BM = 5\) см.

Рассмотрим \(\triangle ASM\): он прямоугольный (\(SM \perp AB\)).
По теореме Пифагора:
\(
SM = \sqrt{SA^2 — AM^2} = \sqrt{10^2 — 5^2} = \sqrt{100 — 25} = \sqrt{75} = 5\sqrt{3} \, \text{см}.
\)

Ответ: \(SM \perp \alpha\).

Дано: треугольник \( \triangle ABC \) прямоугольный, с прямым углом при вершине \( C \). Все стороны \( SA = SB = SC = 10 \) см, а медиана \( CM = 5 \) см. Нужно доказать, что \( SM \perp \alpha \).

Рассмотрим треугольник \( \triangle ASB \). Он равнобедренный, так как \( SA = SB \). В равнобедренном треугольнике медиана, проведенная к основанию, является также и высотой. Это значит, что \( SM \) перпендикулярно \( AB \).

Теперь используем свойство прямоугольного треугольника: медиана, проведенная к гипотенузе, равна её половине. В данном случае медиана \( CM \) равна половине гипотенузы \( AB \), то есть \( CM = AM = BM = 5 \) см.

Далее рассмотрим треугольник \( \triangle ASM \). Он прямоугольный, так как \( SM \perp AB \). Применяем теорему Пифагора для нахождения длины \( SM \):

\( SM = \sqrt{SA^2 — AM^2} \)

Подставляем известные значения:

\( SM = \sqrt{10^2 — 5^2} = \sqrt{100 — 25} = \sqrt{75} = 5\sqrt{3} \) см.

Таким образом, мы доказали, что \( SM \perp \alpha \).