
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 201 Атанасян — Подробные Ответы
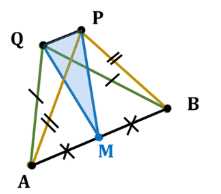
Найдите угол между скрещивающимися прямыми \(AB\) и \(PQ\), если точки \(P\) и \(Q\) равноудалены от концов отрезка \(AB\).
Дано: \(AB \cap PQ = \emptyset\), \(AB \not\parallel PQ\), \(PA = PB\), \(QA = QB\).
Найти: \(\angle(AB, PQ)\).
Решение:
Построим \(M \in AB\), где \(MA = MB\).
Треугольники \(\triangle AQB\) и \(\triangle APB\) равнобедренные по условию, следовательно, медианы \(QM\) и \(PM\), проведенные к основанию \(AB\), являются высотами.
\(QM \perp AB\), \(PM \perp AB \rightarrow AB \perp PQM \rightarrow AB \perp PQ \rightarrow \angle(AB, PQ) = 90^\circ\).
Ответ: \(\angle(AB, PQ) = 90^\circ\).
Дано, что \(AB \cap PQ = \emptyset\), \(AB \not\parallel PQ\), \(PA = PB\), \(QA = QB\). Требуется найти угол между прямыми \(AB\) и \(PQ\).
Сначала строим точку \(M \in AB\), такую, что \(MA = MB\). Точка \(M\) является серединой отрезка \(AB\).
Рассмотрим треугольники \(\triangle AQB\) и \(\triangle APB\). Эти треугольники равнобедренные, так как \(QA = QB\) и \(PA = PB\) по условию. В равнобедренных треугольниках медианы, проведенные к основанию, являются одновременно высотами. Следовательно, отрезки \(QM\) и \(PM\), проведенные к основанию \(AB\), перпендикулярны \(AB\): \(QM \perp AB\) и \(PM \perp AB\).
Так как \(QM \perp AB\) и \(PM \perp AB\), то плоскость, содержащая треугольник \(PQM\), также перпендикулярна прямой \(AB\). Это означает, что прямая \(PQ\), лежащая в этой плоскости, также перпендикулярна \(AB\).
Из этого следует, что угол между прямыми \(AB\) и \(PQ\) равен \(90^\circ\).
Ответ: \(\angle(AB, PQ) = 90^\circ\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!