
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 200 Атанасян — Подробные Ответы
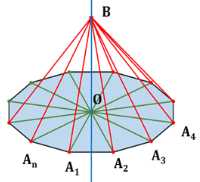
Докажите, что любая точка прямой, которая проходит через центр окружности, описанной около многоугольника, и перпендикулярна к плоскости многоугольника, равноудалена от вершин этого многоугольника.
Дано: \( A_1A_2A_3 \dots A_n \in \mathbb{R} \), \( A_1A_2A_3 \dots A_n \) — \( n \)-угольник, \( O \) — центр описанной окружности, \( OB \perp \text{плоскости} \).
Доказать: Для всех \( i = 1 \dots n, BA_i = \text{const} \).
Решение:
\( O \) — центр описанной окружности, следовательно, для всех \( i = 1 \dots n, OA_i = R \).
Так как \( OB \perp \text{плоскости} \), то \( OB \perp OA_i \) для всех \( i = 1 \dots n \).
Рассмотрим все \(\triangle OBA_i\):
Для всех \( i = 1 \dots n, OA_i = R \), \( OB \) — общая, \(\angle BOA_i = 90^\circ\).
Следовательно, для всех \( i, j = 1 \dots n, \triangle BOA_i \cong \triangle BOA_j \).
Значит, для всех \( i = 1 \dots n, BA_i = \text{const} \).
Ответ: Для всех \( i = 1 \dots n, BA_i = \text{const} \).
Дано, что \(A_1A_2A_3 \dots A_n\) является \(n\)-угольником, лежащим в одной плоскости, и \(O\) — центр описанной окружности этого \(n\)-угольника. Также известно, что \(OB \perp \text{плоскости}\), то есть прямая \(OB\) перпендикулярна плоскости \(n\)-угольника.
Необходимо доказать, что для всех \(i = 1 \dots n\) расстояние \(BA_i\) одинаково, то есть \(BA_i = \text{const}\).
Переходим к доказательству. Центр описанной окружности \(O\) имеет свойство, что расстояние от него до любой вершины \(A_i\) многоугольника одинаково. Это означает, что для всех \(i = 1 \dots n\) выполняется равенство \(OA_i = R\), где \(R\) — радиус описанной окружности.
Далее, так как \(OB \perp \text{плоскости}\), то \(OB\) перпендикулярно любому отрезку \(OA_i\), проведённому от \(O\) к вершинам \(A_i\). Это свойство означает, что угол между \(OB\) и \(OA_i\) равен \(90^\circ\) для всех \(i = 1 \dots n\).
Теперь рассмотрим треугольники \(\triangle OBA_i\) для всех \(i = 1 \dots n\). В каждом из этих треугольников:
1. \(OA_i = R\), так как это радиус описанной окружности.
2. \(OB\) является общей стороной для всех треугольников.
3. Угол \(\angle BOA_i = 90^\circ\) для всех \(i = 1 \dots n\), так как \(OB \perp OA_i\).
На основании этих трёх свойств можно заключить, что все треугольники \(\triangle OBA_i\) равны друг другу по первому признаку равенства треугольников (гипотенуза и острый угол). Из равенства треугольников следует, что все стороны \(BA_i\) равны между собой. То есть для всех \(i = 1 \dots n\) выполняется равенство \(BA_i = \text{const}\).
Таким образом, доказано, что расстояние от точки \(B\) до любой вершины \(A_i\) многоугольника одинаково.
Ответ: для всех \(i = 1 \dots n, BA_i = \text{const}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!