
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 20 Атанасян — Подробные Ответы
Средняя линия трапеции лежит в плоскости \(\alpha\). Пересекают ли прямые, содержащие её основания, плоскость \(\alpha\)? Ответ обоснуйте.
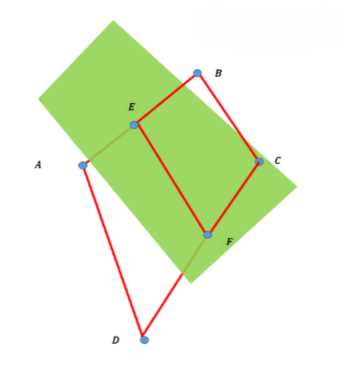
Дано: \(EF \subset \alpha\), \(EF\) — средняя линия трапеции \(ABCD\), \(EF \parallel BC\) и \(EF \parallel AD\).
По теореме, если прямая, не лежащая в плоскости, параллельна прямой, лежащей в этой плоскости, то она пересекает данную плоскость.
Следовательно, \(BC \cap \alpha \neq \emptyset\) и \(AD \cap \alpha \neq \emptyset\).
Ответ: \(
BC \cap \alpha \neq \emptyset, \quad AD \cap \alpha \neq \emptyset.
\)
Дано: \(ABCD\) — трапеция, \(EF\) — её средняя линия, которая лежит в плоскости \(\alpha\). Требуется доказать, что прямые, содержащие основания \(BC\) и \(AD\), пересекают плоскость \(\alpha\).
Средняя линия трапеции \(EF\) параллельна основаниям \(BC\) и \(AD\), то есть \(EF \parallel BC\) и \(EF \parallel AD\).
Поскольку \(EF \subset \alpha\), то \(EF\) лежит в плоскости \(\alpha\).
По теореме: если прямая, не лежащая в данной плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то эта прямая пересекает данную плоскость. Применим эту теорему к основаниям трапеции:
1. Прямая \(BC\) параллельна \(EF\), а \(EF \subset \alpha\). Следовательно, \(BC\) пересекает плоскость \(\alpha\).
2. Прямая \(AD\) также параллельна \(EF\), а \(EF \subset \alpha\). Следовательно, \(AD\) пересекает плоскость \(\alpha\).
Таким образом, обе прямые \(BC\) и \(AD\) пересекают плоскость \(\alpha\).
Ответ: \(
BC \cap \alpha \neq \emptyset, \quad AD \cap \alpha \neq \emptyset.
\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!