
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 199 Атанасян — Подробные Ответы
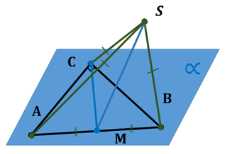
Точка \(S\) равноудалена от вершин прямоугольного треугольника и не лежит в плоскости этого треугольника. Докажите, что прямая \(SM\), где \(M\) — середина гипотенузы, перпендикулярна к плоскости треугольника
Дано:
\( \triangle ABC \) — прямоугольный, \( \angle C = 90^\circ \), \( SA = SB = SC \), \( AM = MB \).
Доказать: \( SM \perp \alpha \).
Решение:
По построению очевидно, что \( \triangle ASB \) — равнобедренный, поэтому медиана, проведенная к основанию, является высотой: \( SM \perp AB \).
По свойству прямоугольного \( \triangle ABC \), медиана, проведенная к гипотенузе, равна её половине:
\( CM = AM = BM \).
Рассмотрим \( \triangle ASM \) и \( \triangle CSM \):
\( AS = CS \) по условию, \( AM = CM \), \( SM \) — общая сторона.
Следовательно, \( \triangle ASM \cong \triangle CSM \), а \( \angle CMS = \angle AMS = 90^\circ \), так как \( SM \perp AB \).
Таким образом, \( SM \perp AB \), \( SM \perp CM \), значит \( SM \perp \alpha \).
Ответ: \( SM \perp \alpha \).
Дано, что треугольник \( \triangle ABC \) прямоугольный, угол \( \angle C = 90^\circ \), а отрезки \( SA = SB = SC \). Также известно, что медиана \( AM \) равна медиане \( BM \), то есть \( AM = MB \). Требуется доказать, что отрезок \( SM \) перпендикулярен плоскости \( \alpha \), в которой лежит треугольник \( \triangle ABC \).
Сначала рассмотрим треугольник \( \triangle ASB \). Этот треугольник равнобедренный, так как по условию \( SA = SB \). В равнобедренном треугольнике медиана, проведенная к основанию, одновременно является высотой. Следовательно, медиана \( SM \), проведенная к основанию \( AB \), перпендикулярна этому основанию, то есть \( SM \perp AB \).
Далее используем свойство прямоугольного треугольника \( \triangle ABC \). В любом прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине длины гипотенузы. Так как гипотенуза \( AB \) делится медианой \( CM \) на два равных отрезка, то \( CM = AM = BM \).
Теперь рассмотрим два треугольника \( \triangle ASM \) и \( \triangle CSM \). По условию \( AS = CS \), так как \( SA = SC \). Также \( AM = CM \), как было доказано ранее, и \( SM \) является общей стороной для обоих треугольников. Таким образом, треугольники \( \triangle ASM \) и \( \triangle CSM \) равны по двум сторонам и углу между ними.
Из равенства треугольников следует, что углы \( \angle CMS \) и \( \angle AMS \) равны и оба являются прямыми, то есть \( \angle CMS = \angle AMS = 90^\circ \). Это означает, что отрезок \( SM \) перпендикулярен как основанию \( AB \), так и медиане \( CM \).
Так как \( SM \) перпендикулярен двум пересекающимся прямым \( AB \) и \( CM \), лежащим в плоскости \( \alpha \), то \( SM \) перпендикулярен всей плоскости \( \alpha \).
Таким образом, доказано, что \( SM \perp \alpha \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!