
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 196 Атанасян — Подробные Ответы
Изобразите куб \(ABCDA_1B_1C_1D_1\) и постройте его сечение плоскостью, проходящей через:
а) ребро \(AA_1\) и перпендикулярной к плоскости \(BB_1D_1\);
б) ребро \(AB\) и перпендикулярной к плоскости \(CDA_1\).
Дано: \( ABCDA_1B_1C_1D_1 \) — куб.
Построить:
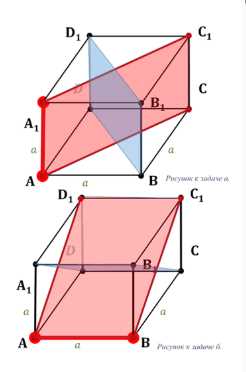
а) сечение плоскостью через \( AA_1 \), перпендикулярно \( BB_1D \);
б) сечение плоскостью через \( AB \), перпендикулярно \( CDA_1 \).
Решение:
Обе задачи симметричны с точностью до обозначений или поворота куба. Перпендикулярность построенных плоскостей очевидна, так как линейные углы соответствующих двугранных углов проходят через диагонали квадрата — грани куба (\( A_1B_1C_1D_1 \) в случае а) и грани куба (\( BB_1C_1 \) в случае б).
Ответ: на рисунках.
Дано куб \( ABCDA_1B_1C_1D_1 \). Необходимо построить сечения плоскостями в двух случаях:
а) через прямую \( AA_1 \), перпендикулярно плоскости, содержащей точки \( BB_1D \);
б) через прямую \( AB \), перпендикулярно плоскости, содержащей точки \( CDA_1 \).
Рассмотрим случай а.
Плоскость должна проходить через прямую \( AA_1 \), то есть через вершины \( A \) и \( A_1 \). Кроме того, она должна быть перпендикулярна плоскости, содержащей точки \( BB_1D \). Плоскость \( BB_1D \) пересекает грань куба \( ABB_1A_1 \) по диагонали \( BB_1 \), а также пересекает грань \( BCC_1B_1 \) по диагонали \( B_1D \). Таким образом, искомая плоскость будет проходить через прямую \( AA_1 \) и пересекать грани куба параллельно диагоналям, образующим плоскость \( BB_1D \). Линии пересечения плоскости с гранями \( ABB_1A_1 \) и \( BCC_1B_1 \) будут параллельны диагоналям \( BB_1 \) и \( B_1D \), соответственно. Это определяет положение сечения, и его построение можно выполнить, соединив соответствующие точки пересечения.
Рассмотрим случай б.
Плоскость должна проходить через прямую \( AB \), то есть через вершины \( A \) и \( B \). Кроме того, она должна быть перпендикулярна плоскости, содержащей точки \( CDA_1 \). Плоскость \( CDA_1 \) пересекает грань куба \( ABCD \) по диагонали \( AC \), а также пересекает грань \( CDA_1D_1 \) по диагонали \( DA_1 \). Искомая плоскость будет проходить через прямую \( AB \) и пересекать грани куба параллельно диагоналям, образующим плоскость \( CDA_1 \). Линии пересечения плоскости с гранями \( ABCD \) и \( CDA_1D_1 \) будут параллельны диагоналям \( AC \) и \( DA_1 \), соответственно. Это определяет положение сечения, и его построение можно выполнить, соединив соответствующие точки пересечения.
Таким образом, для обоих случаев сечения определяются симметрично, с учетом указанных условий перпендикулярности и прохождения через заданные прямые.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!