
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 194 Атанасян — Подробные Ответы
Ребро куба равно \(a\). Найдите расстояние между скрещивающимися прямыми, содержащими:
а) диагональ куба и ребро куба;
б) диагональ куба и диагональ грани куба.
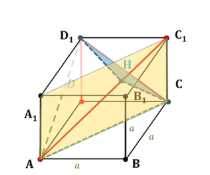
Дано: \( ABCDA_1B_1C_1D_1 \) — куб со стороной \( a \).
a) \( DD_1 \parallel AC_1 \). Расстояние между ними равно расстоянию от любой точки \( DD_1 \), например \( D \), до плоскости \( ACC_1 \). Это высота треугольника \( \triangle ADC \), равная половине диагонали грани:
\(
d = \frac{a \sqrt{2}}{2}.
\)
b) Построим \( \triangle HCD_1 \), где \( H \) — точка пересечения перпендикуляров из \( C \) и \( D_1 \) к \( AC_1 \). Расстояние между \( AC_1 \) и \( CD_1 \) — высота \( \triangle HCD_1 \), равная его медиане. По теореме Пифагора:
\(
h_{AC_1D_1} = \sqrt{\frac{a^2}{2} — \left(\frac{a \sqrt{2}}{2}\right)^2} = \sqrt{\frac{a^2}{6}} = \frac{a}{\sqrt{6}}.
\)
Ответ:
a) \( = \frac{a}{\sqrt{2}} \),
b) \( \frac{a}{\sqrt{6}} \).
Дано: \( ABCDA_1B_1C_1D_1 \) — куб со стороной \( a \). Необходимо найти расстояние между прямыми \( AC_1 \) и \( DD_1 \), а также между \( AC_1 \) и \( CD_1 \).
Рассмотрим задачу нахождения расстояния между \( AC_1 \) и \( DD_1 \). Так как \( DD_1 \parallel AA_1 \), а \( AC_1 \) также пересекает плоскость, перпендикулярную \( AA_1 \), то прямые \( DD_1 \) и \( AC_1 \) параллельны и не лежат в одной плоскости. Чтобы найти расстояние между ними, достаточно определить расстояние от любой точки прямой \( DD_1 \) до плоскости \( ACC_1 \). Например, возьмем точку \( D \).
Точка \( D \) лежит в одной плоскости с точками \( A \), \( C \), \( D_1 \). Расстояние от точки \( D \) до плоскости \( ACC_1 \) совпадает с высотой треугольника \( \triangle ADC \), который является равнобедренным прямоугольным треугольником. В этом треугольнике гипотенуза равна диагонали грани куба \( \sqrt{a^2 + a^2} = a\sqrt{2} \), а высота, проведенная к гипотенузе, равна половине этой диагонали:
\(
d = \frac{a\sqrt{2}}{2}.
\)
Теперь рассмотрим задачу нахождения расстояния между \( AC_1 \) и \( CD_1 \). Построим треугольник \( \triangle HCD_1 \), где \( H \) — точка пересечения перпендикуляров, опущенных из точек \( C \) и \( D_1 \) на прямую \( AC_1 \). Очевидно, что расстояние между прямыми \( AC_1 \) и \( CD_1 \) равно высоте \( \triangle HCD_1 \).
Для нахождения высоты \( \triangle HCD_1 \) выразим его стороны. Точка \( H \) находится на прямой \( AC_1 \), и расстояние \( HC \) от \( C \) до \( AC_1 \) является высотой треугольника \( \triangle ACC_1 \). В этом треугольнике катеты равны \( a \), а гипотенуза равна \( a\sqrt{2} \). Тогда высота \( HC \) вычисляется по формуле:
\(
HC = \frac{\text{катет}_1 \cdot \text{катет}_2}{\text{гипотенуза}} = \frac{a \cdot a}{a\sqrt{2}} = \frac{a}{\sqrt{2}}.
\)
Рассмотрим \( CD_1 \). Его длина равна диагонали грани куба и равна \( a\sqrt{2} \). Высота \( h_{AC_1D_1} \) — это медиана \( \triangle HCD_1 \), которую можно найти по формуле:
\(
h_{AC_1D_1}^2 = HC^2 — \left(\frac{CD_1}{2}\right)^2.
\)
Подставим значения. \( HC = \frac{a}{\sqrt{2}} \), а \( \frac{CD_1}{2} = \frac{a\sqrt{2}}{2} = \frac{a}{\sqrt{2}}\):
\(
h_{AC_1D_1}^2 = \left(\frac{a}{\sqrt{2}}\right)^2 — \left(\frac{a\sqrt{2}}{2}\right)^2.
\)
Выполним вычисления:
\(
h_{AC_1D_1}^2 = \frac{a^2}{2} — \frac{a^2 \cdot 2}{4} = \frac{a^2}{2} — \frac{a^2}{2 \cdot 2} = \frac{a^2}{6}.
\)
Тогда:
\(
h_{AC_1D_1} = \sqrt{\frac{a^2}{6}} = \frac{a}{\sqrt{6}}.
\)
Ответ:
a) \( \frac{a}{\sqrt{2}} \),
b) \( \frac{a}{\sqrt{6}} \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!