Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 193 Атанасян — Подробные Ответы
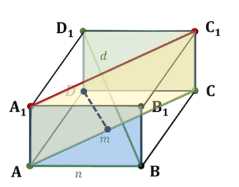
В прямоугольном параллелепипеде \(ABCDA_1B_1C_1D_1\) дано: \(D_1B = d\), \(AC = m\), \(AB = n\). Найдите расстояние между:
а) прямой \(A_1C_1\) и плоскостью \(ABC\);
б) плоскостями \(ABB_1\) и \(DCC_1\);
в) прямой \(DD_1\) и плоскостью \(ACC_1\).
Дано: прямоугольный параллелепипед \(ABCD A_1B_1C_1D_1\), где \(D_1B = d\), \(AC = m\), \(AB = n\).
Найти расстояния:
\(a)\) между \(A_1C_1\) и \(ABCD\),
\(b)\) между \(ABB_1\) и \(DCC_1\),
\(c)\) между \(D_1D\) и \(ACC_1\).
Решение:
По теореме Пифагора:
\(
D_1D = \sqrt{d^2 — m^2}, \quad BC = \sqrt{m^2 — n^2}.
\)
Третье расстояние \(h\) — это высота треугольника \(\triangle ADC\), выражается через стороны:
\(
h = n \cdot \sqrt{1 — \left(\frac{m}{d}\right)^2}.
\)
Ответ:
\(
D_1D = \sqrt{d^2 — m^2}, \quad BC = \sqrt{m^2 — n^2}, \quad h = n \cdot \sqrt{1 — \left(\frac{m}{d}\right)^2}.
\)
Дано прямоугольный параллелепипед \(ABCD A_1B_1C_1D_1\), где \(D_1B = d\), \(AC = m\), \(AB = n\). Требуется найти три расстояния.
Для нахождения расстояния между точками или плоскостями используется теорема Пифагора и геометрические свойства параллелепипеда.
Сначала определим расстояние \(D_1D\). Это расстояние является диагональю прямоугольного треугольника \(\triangle BDD_1\), где гипотенуза \(D_1D\), а катеты \(BD\) и \(D_1B\). Катет \(BD\) равен диагонали основания прямоугольного параллелограмма \(ABCD\), которая равна \(m\). Катет \(D_1B\) равен \(d\). По теореме Пифагора:
\(D_1D = \sqrt{d^2 — m^2}\).
Далее определим расстояние \(BC\). Это расстояние является одной из сторон основания параллелепипеда \(ABCD\). Основание представляет собой прямоугольник, где стороны \(AB = n\) и \(BC = \sqrt{m^2 — n^2}\). Это значение также находится по теореме Пифагора, так как диагональ основания \(AC = m\), а одна из сторон \(AB = n\).
Теперь вычислим расстояние \(h\) между прямой \(D_1D\) и плоскостью \(ACC_1\). Это расстояние равно высоте треугольника \(\triangle ADC\), проведенной из вершины \(A\) на сторону \(DC\). Для нахождения высоты используется формула:
\(h = n \cdot \sqrt{1 — \left(\frac{m}{d}\right)^2}\),
где \(n\) — длина стороны \(AB\), а \(\frac{m}{d}\) — отношение сторон, связанное с углами наклона треугольника.
Таким образом, ответы находятся через применение теоремы Пифагора и геометрических соотношений. Итоговые значения:
\(D_1D = \sqrt{d^2 — m^2}\),
\(BC = \sqrt{m^2 — n^2}\),
\(h = n \cdot \sqrt{1 — \left(\frac{m}{d}\right)^2}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.