
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 191 Атанасян — Подробные Ответы
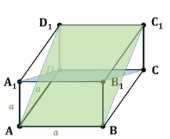
Дан куб \(ABCDA_1B_1C_1D_1\). Докажите, что плоскости \(ABC_1\) и \(A_1B_1D\) перпендикулярны.
Дано: \( ABCDA_1B_1C_1D_1 \) — куб со стороной \( a \).
Доказать: \( ABC_1 \perp A_1B_1D \).
Решение:
Очевидно, что по свойству куба \( ABC_1 \perp B_1C_1C \), и \( A_1B_1D \perp B_1C_1C \).
Рассмотрим \( BB_1C_1C \) в плоскости \( (B_1C_1C) \): по свойству куба это квадрат, диагонали которого перпендикулярны. С другой стороны, по свойству куба эти диагонали образуют стороны линейного угла между плоскостями \( ABC_1 \) и \( A_1B_1D \).
Следовательно, \( ABC_1 \perp A_1B_1D \).
Ответ: \( ABC_1 \perp A_1B_1D \).
Дано: \( ABCDA_1B_1C_1D_1 \) — куб со стороной \( a \).
Доказать: \( ABC_1 \perp A_1B_1D \).
Рассмотрим свойства куба. Куб — это правильный многогранник, у которого все грани являются квадратами, а все ребра равны. В кубе любые смежные грани перпендикулярны друг другу.
Плоскость \( ABC_1 \) проходит через вершины \( A, B \) и \( C_1 \). Плоскость \( A_1B_1D \) проходит через вершины \( A_1, B_1 \) и \( D \). Необходимо доказать, что данные плоскости перпендикулярны.
Рассмотрим проекцию обеих плоскостей на плоскость \( (B_1C_1C) \). Эта плоскость является одной из граней куба, и она представляет собой квадрат. Диагонали квадрата \( B_1C_1C \) пересекаются под прямым углом.
Плоскость \( ABC_1 \) содержит диагональ \( B_1C_1 \), которая лежит в плоскости \( (B_1C_1C) \). Плоскость \( A_1B_1D \) содержит диагональ \( BB_1 \), которая также лежит в плоскости \( (B_1C_1C) \).
Таким образом, в квадрате \( B_1C_1C \) диагонали \( B_1C_1 \) и \( BB_1 \) пересекаются под прямым углом. Это означает, что линейный угол между плоскостями \( ABC_1 \) и \( A_1B_1D \) равен \( 90^\circ \).
Следовательно, \( ABC_1 \perp A_1B_1D \).
Ответ: \( ABC_1 \perp A_1B_1D \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!