
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 190 Атанасян — Подробные Ответы
Дан куб \(ABCDA_1B_1C_1D_1\). Найдите следующие двугранные углы:
а) \(ABB_1C\);
б) \(ADD_1B\);
в) \(A_1BB_1K\), где \(K\) — середина ребра \(A_1D_1\).
\(\angle ABB_1C = 90^\circ\), так как грани куба перпендикулярны.
\(\angle ADD_1B = 45^\circ\), так как диагонали грани куба образуют угол \(45^\circ\).
\(\angle ABB_1K = \arctan\left(\frac{1}{2}\right)\), так как \(\tan\) угла определяется как отношение катетов.
Рассмотрим куб \( ABCDA_1B_1C_1D_1 \) со стороной \( a \). Найдем заданные двугранные углы.
Двугранный угол \(\angle ABB_1C\) образован гранями \( ABCD \) и \( ABB_1B_1 \). Эти две грани перпендикулярны, так как одна из них горизонтальная (\(ABCD\)), а другая вертикальная (\(ABB_1B_1\)). Угол между такими гранями всегда равен \( 90^\circ \). Следовательно, \(\angle 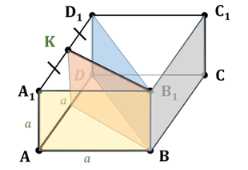
Двугранный угол \(\angle ADD_1B\) образован гранями \( ABCD \) и \( ADD_1D_1 \). Грань \( ADD_1D_1 \) вертикальная, а \( ABCD \) горизонтальная. Если рассмотреть диагонали этих граней, то диагональ \( AD \) в горизонтальной плоскости образует угол \( 45^\circ \) с диагональю \( AB \). Этот угол равен \( 45^\circ \), так как грани куба симметричны. Следовательно, \(\angle ADD_1B = 45^\circ\).
Двугранный угол \(\angle ABB_1K\) образован гранями \( ABB_1B_1 \) и \( ABB_1K \). Точка \( K \) делит диагональ \( AD_1 \) пополам, поэтому \( AK = KD_1 = \frac{a}{2} \). В треугольнике \( ABB_1 \), где \( AB = a \), можно рассмотреть отношение \(\tan\) угла между плоскостями. Для этого находим отношение \( \frac{A_1K}{AB} = \frac{\frac{a}{2}}{a} = \frac{1}{2} \). Таким образом, угол между гранями равен \(\arctan\left(\frac{1}{2}\right)\).
Ответ: \(\angle ABB_1C = 90^\circ\), \(\angle ADD_1B = 45^\circ\), \(\angle ABB_1K = \arctan\left(\frac{1}{2}\right)\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!