ГДЗ по Геометрии 10 класс Номер 189 Атанасян — Подробные Ответы

Найдите расстояние от вершины куба до плоскости любой грани, в которой не лежит эта вершина, если:
а) диагональ грани куба равна \(m\);
б) диагональ куба равна \(d\).

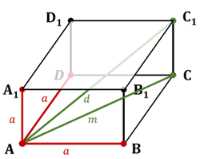
Дано: \(ABCD A_1B_1C_1D_1\) — куб со стороной \(a\), диагональ куба \(AC_1 = d\), диагональ грани \(AC = m\).

Найти: расстояние от вершины куба до сторон, не содержащих данную вершину.

Решение:
Очевидно, что расстояние равно стороне куба \(a\). Используя формулы для диагоналей:
\(
AC = m = a\sqrt{2}, \quad AC_1 = d = a\sqrt{3}
\)
выражаем \(a\):
\(
a = \frac{d}{\sqrt{3}}, \quad a = \frac{m}{\sqrt{2}}
\)

Ответ: \(a = \frac{d}{\sqrt{3}}, \, a = \frac{m}{\sqrt{2}}\).

Дано: куб \( ABCD A_1B_1C_1D_1 \) со стороной \( a \), диагональ куба \( AC_1 = d \), диагональ грани \( AC = m \). Необходимо найти расстояние от вершины куба до сторон, не содержащих данную вершину.

Рассмотрим вершину \( A \). Нам нужно найти расстояние от этой вершины до сторон, которые не содержат \( A \). Очевидно, такими сторонами являются \( A_1B_1, B_1C_1 \) и \( C_1D_1 \). Расстояние от вершины \( A \) до любой из этих сторон совпадает с длиной стороны куба \( a \), так как они перпендикулярны соответствующим плоскостям.

Для проверки используется связь между сторонами, диагональю грани и диагональю куба. По теореме Пифагора:
\(
AC^2 = AB^2 + BC^2 = a^2 + a^2 = 2a^2
\)
\(
AC = m = a\sqrt{2}
\)

Также по теореме Пифагора:
\(
AC_1^2 = AC^2 + CC_1^2 = m^2 + a^2 = 2a^2 + a^2 = 3a^2
\)
\(
AC_1 = d = a\sqrt{3}
\)

Теперь, выражая сторону \( a \) через заданные величины \( d \) и \( m \), получаем:
\(
a = \frac{d}{\sqrt{3}}, \quad a = \frac{m}{\sqrt{2}}
\)

Таким образом, расстояние от вершины куба до сторон, не содержащих её, равно стороне куба \( a \), которая может быть выражена через \( d \) или \( m \) в зависимости от условий.