
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 188 Атанасян — Подробные Ответы
Ребро куба равно \(a\). Найдите диагональ куба.
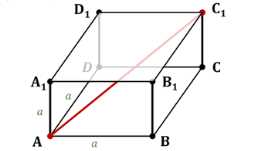
Дано: \(ABCD A_1B_1C_1D_1\) — куб со стороной \(a\). Найти: диагональ куба \(AC_1\).
Решение:
Применяя теорему Пифагора к \(\triangle ABC\) и \(\triangle ACC_1\), последовательно имеем:
\(
AC_1^2 = AC^2 + CC_1^2 = (AB^2 + BC^2) + CC_1^2 = a^2 + a^2 + a^2 = 3 \cdot a^2
\)
\(
AC_1 = a \cdot \sqrt{3}
\)
Ответ: \(a \cdot \sqrt{3}\).
Рассмотрим куб со стороной a. Необходимо найти диагональ куба AC₁, которая соединяет вершину A основания куба с противоположной вершиной C₁ верхней грани.
Для этого применим теорему Пифагора дважды. Сначала найдем диагональ основания куба AC, а затем, используя её, найдем диагональ всего куба AC₁.
Сначала рассмотрим треугольник ABC, лежащий в основании куба. В этом треугольнике стороны AB и BC равны a, так как это стороны куба. По теореме Пифагора для треугольника ABC:
AC² = AB² + BC²
AC² = a² + a²
AC² = 2a²
AC = √(2a²) = a√2.
Теперь рассмотрим треугольник ACC₁, где AC – диагональ основания, а CC₁ – ребро куба, равное a. По теореме Пифагора для этого треугольника:
AC₁² = AC² + CC₁²
AC₁² = (a√2)² + a²
AC₁² = 2a² + a²
AC₁² = 3a²
AC₁ = √(3a²) = a√3.
Таким образом, длина диагонали куба AC₁ равна a√3.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!