ГДЗ по Геометрии 10 класс Номер 186 Атанасян — Подробные Ответы

Докажите, что существует, и притом только одна, прямая, пересекающая две данные скрещивающиеся прямые \(a\) и \(b\) и перпендикулярная к каждой из них.
Решение

Рассмотрим плоскость \(\alpha\), проходящую через прямую \(a\) и параллельную прямой \(b\). Через прямые \(a\) и \(b\) проведём плоскости \(\beta\) и \(\gamma\) так, чтобы \(\beta \perp \alpha\) и \(\gamma \perp \alpha\) (задача 185). Докажите самостоятельно, что прямая \(r\), по которой пересекаются плоскости \(\beta\) и \(\gamma\), искомая. Докажем, что \(r\) — единственная прямая, удовлетворяющая условию задачи.
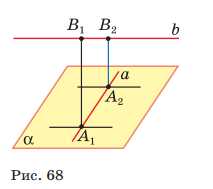
Предположим, что существуют две прямые \(A_1B_1\) и \(A_2B_2\), пересекающие данные скрещивающиеся прямые \(a\) и \(b\) и перпендикулярные к каждой из них (рис. 68). Прямые \(A_1B_1\) и \(A_2B_2\) перпендикулярны к плоскости \(\alpha\) (объясните почему), поэтому они параллельны. Отсюда следует, что скрещивающиеся прямые \(a\) и \(b\) лежат в одной плоскости, что противоречит определению скрещивающихся прямых.

Рассмотрим плоскость \(\alpha\), проходящую через прямую \(a\) и параллельную прямой \(b\). Через прямые \(a\) и \(b\) проведём плоскости \(\beta\) и \(\gamma\) так, чтобы \(\beta \perp \alpha\) и \(\gamma \perp \alpha\). Прямая \(r\), по которой пересекаются плоскости \(\beta\) и \(\gamma\), искомая, так как она перпендикулярна плоскости \(\alpha\), а значит, перпендикулярна и прямым \(a\) и \(b\).

Докажем единственность. Предположим, что существуют две такие прямые \(A_1B_1\) и \(A_2B_2\). Они перпендикулярны плоскости \(\alpha\), поэтому параллельны. Но тогда \(a\) и \(b\) лежат в одной плоскости, что противоречит определению скрещивающихся прямых. Следовательно, прямая \(r\) единственна.

Рассмотрим две данные скрещивающиеся прямые \(a\) и \(b\). По определению, скрещивающиеся прямые не лежат в одной плоскости и не пересекаются.

Пусть \(\alpha\) — плоскость, проходящая через прямую \(a\) и параллельная прямой \(b\). Такая плоскость существует, так как для любой прямой можно провести плоскость, содержащую её, и через эту же плоскость можно провести параллельную прямую. Прямая \(b\), будучи параллельной \(\alpha\), не пересекает её, но не лежит в самой плоскости \(\alpha\).

Теперь проведём плоскость \(\beta\) через прямую \(a\), перпендикулярную плоскости \(\alpha\). Такая плоскость существует по свойству перпендикулярности. Аналогично, проведём плоскость \(\gamma\) через прямую \(b\), перпендикулярную плоскости \(\alpha\). Таким образом, плоскости \(\beta\) и \(\gamma\) обе перпендикулярны плоскости \(\alpha\).

Поскольку плоскости \(\beta\) и \(\gamma\) пересекаются, их пересечение образует прямую \(r\). Прямая \(r\) лежит одновременно в плоскости \(\beta\) и в плоскости \(\gamma\). Это означает, что \(r\) перпендикулярна плоскости \(\alpha\), так как обе плоскости \(\beta\) и \(\gamma\) перпендикулярны \(\alpha\). Следовательно, прямая \(r\) перпендикулярна и прямой \(a\), и прямой \(b\), так как \(a\) и \(b\) лежат в соответствующих плоскостях \(\beta\) и \(\gamma\), перпендикулярных \(\alpha\).

Докажем единственность прямой \(r\). Предположим, что существуют две разные прямые \(A_1B_1\) и \(A_2B_2\), которые пересекают прямые \(a\) и \(b\) и перпендикулярны к каждой из них. Эти прямые \(A_1B_1\) и \(A_2B_2\) должны быть перпендикулярны плоскости \(\alpha\), так как они перпендикулярны прямым \(a\) и \(b\), лежащим в плоскости \(\alpha\). Однако, если \(A_1B_1\) и \(A_2B_2\) обе перпендикулярны плоскости \(\alpha\), то они параллельны между собой. Это означает, что \(a\) и \(b\) должны лежать в одной плоскости, что противоречит определению скрещивающихся прямых. Следовательно, предположение о существовании двух различных прямых \(A_1B_1\) и \(A_2B_2\) неверно.

Таким образом, существует только одна прямая \(r\), которая пересекает данные скрещивающиеся прямые \(a\) и \(b\) и перпендикулярна к каждой из них.