ГДЗ по Геометрии 10 класс Номер 184 Атанасян — Подробные Ответы

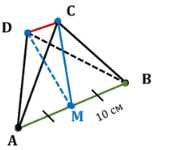
Общая сторона \(AB\) треугольников \(ABC\) и \(ABD\) равна \(10 \, \text{см}\). Плоскости этих треугольников взаимно перпендикулярны. Найдите \(CD\), если треугольники:
а) равносторонние;
б) прямоугольные равнобедренные с гипотенузой \(AB\).

Дано: \(AB = 10 \, \text{см}\), \(\angle (ABC, ABD) = 90^\circ\).
Найти: \(CD\), если \(\triangle ABC\) и \(\triangle ABD\) равносторонние или прямоугольные равнобедренные с гипотенузой \(AB\).

Рассмотрим \(\triangle ABC\) и \(\triangle ABD\).
Так как треугольники равны, медианы \(DM = CM\).
В случае равностороннего треугольника высота равна \(\frac{\sqrt{3}}{2} \cdot AB = 5 \cdot \sqrt{3} \, \text{см}\).
В случае прямоугольного равнобедренного треугольника высота равна \(\frac{AB}{2} = 5 \, \text{см}\).

По теореме Пифагора:
\(
DC = \sqrt{DM^2 + CM^2} = CM \cdot \sqrt{2}.
\)

Подставляем значения:
— Для равностороннего треугольника \(CD = 5 \cdot \sqrt{6} \, \text{см}\).
— Для прямоугольного равнобедренного треугольника \(CD = 5 \cdot \sqrt{2} \, \text{см}\).

Ответ: \(5 \cdot \sqrt{6} \, \text{см}\) и \(5 \cdot \sqrt{2} \, \text{см}\).

Дано, что \(AB = 10 \, \text{см}\) и \(\angle (ABC, ABD) = 90^\circ\). Необходимо найти \(CD\), если треугольники \(\triangle ABC\) и \(\triangle ABD\) либо равносторонние, либо прямоугольные равнобедренные с гипотенузой \(AB\).

Рассмотрим треугольники \(\triangle ABC\) и \(\triangle ABD\). Они равны либо по третьему, либо по второму признаку равенства треугольников. Из этого следует равенство соответствующих медиан: \(DM = CM\).

Проведем медиану \(CM\) в треугольнике \(\triangle ABC\). Если \(\triangle ABC\) равносторонний, то медиана \(CM\) одновременно является высотой и биссектрисой. Аналогично, в треугольнике \(\triangle ABD\) медиана \(DM\) также является высотой и биссектрисой. Поскольку \(\angle CMD = 90^\circ\), медианы \(CM\) и \(DM\) перпендикулярны.

По теореме Пифагора для треугольника \(\triangle DCM\) имеем:
\(
DC = \sqrt{DM^2 + CM^2}
\)

Теперь необходимо найти длину медианы \(CM\) в зависимости от типа треугольника.

Если \(\triangle ABC\) равносторонний, то высота равна \(\frac{\sqrt{3}}{2} \cdot AB\). Подставляем \(AB = 10 \, \text{см}\):
\(
CM = \frac{\sqrt{3}}{2} \cdot 10 = 5 \cdot \sqrt{3} \, \text{см}
\)

Если \(\triangle ABC\) прямоугольный равнобедренный, то высота равна половине гипотенузы. Подставляем \(AB = 10 \, \text{см}\):
\(
CM = \frac{10}{2} = 5 \, \text{см}
\)

Теперь найдем \(DC\) для каждого случая.
Для равностороннего треугольника:
\(
DC = \sqrt{CM^2 + CM^2} = CM \cdot \sqrt{2} = 5 \cdot \sqrt{3} \cdot \sqrt{2} = 5 \cdot \sqrt{6} \, \text{см}
\)

Для прямоугольного равнобедренного треугольника:
\(
DC = \sqrt{CM^2 + CM^2} = CM \cdot \sqrt{2} = 5 \cdot \sqrt{2} \, \text{см}
\)

Таким образом, \(CD = 5 \cdot \sqrt{6} \, \text{см}\) для равностороннего треугольника и \(CD = 5 \cdot \sqrt{2} \, \text{см}\) для прямоугольного равнобедренного треугольника.