
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 183 Атанасян — Подробные Ответы
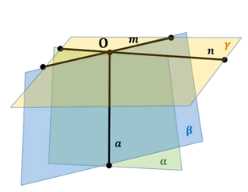
Плоскости \(\alpha\) и \(\beta\) пересекаются по прямой \(a\) и перпендикулярны к плоскости \(\gamma\). Докажите, что прямая \(a\) перпендикулярна к плоскости \(\gamma\).
Дано: \(\alpha \subset \beta\), \(\alpha \subset \gamma\), \(\beta \perp \gamma\).
Доказать: \(a \perp \gamma\).
Решение:
Возьмем точку \(O: O = a \cap \gamma\).
\(n = \alpha \cap \gamma; O = a \cap n; \alpha \perp \beta \Rightarrow \beta \perp n \Rightarrow a \perp n\) (подробно в задаче 181).
\(m = \beta \cap \gamma; O = a \cap m; \alpha \perp \beta \Rightarrow \alpha \perp m \Rightarrow a \perp m\) (подробно в задаче 181).
Так как \(a \perp n\), \(a \perp m\), \(n \subset \gamma\), \(m \subset \gamma\), \(n \cap m = a \perp \gamma\).
Ответ: \(a \perp \gamma\).
Дано: \(\alpha \subset \beta\), \(\alpha \subset \gamma\), \(\beta \perp \gamma\). Нужно доказать, что \(a \perp \gamma\).
Начнем с выбора точки \(O\), которая является пересечением прямой \(a\) и плоскости \(\gamma\), то есть \(O = a \cap \gamma\).
Рассмотрим линию \(n\), которая является пересечением плоскостей \(\alpha\) и \(\gamma\), то есть \(n = \alpha \cap \gamma\). Точка \(O\) также лежит на \(n\), так как \(O = a \cap n\).
Поскольку \(\alpha \subset \beta\) и \(\alpha \perp \beta\), следует, что \(\beta \perp n\). Из этого следует, что \(a \perp n\), так как \(a\) перпендикулярна любой линии, перпендикулярной \(\beta\).
Теперь рассмотрим линию \(m\), которая является пересечением плоскостей \(\beta\) и \(\gamma\), то есть \(m = \beta \cap \gamma\). Точка \(O\) также лежит на \(m\), так как \(O = a \cap m\).
Поскольку \(\alpha \perp \beta\), следует, что \(\alpha \perp m\). Из этого следует, что \(a \perp m\), так как \(a\) перпендикулярна любой линии, перпендикулярной \(\alpha\).
Так как \(n \subset \gamma\) и \(m \subset \gamma\), а также \(n \cap m = a\), то \(a \perp \gamma\).
Таким образом, мы доказали, что \(a\) перпендикулярна \(\gamma\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!