Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 182 Атанасян — Подробные Ответы
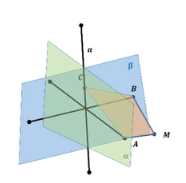
Плоскости \(\alpha\) и \(\beta\) взаимно перпендикулярны и пересекаются по прямой \(a\). Из точки \(M\) проведены перпендикуляры \(MA\) и \(MB\) к этим плоскостям. Прямая \(a\) пересекает плоскость \(AMB\) в точке \(C\).
а) Докажите, что четырёхугольник \(ACBM\) является прямоугольником.
б) Найдите расстояние от точки \(M\) до прямой \(a\), если \(AM = m\), \(BM = n\).
Дано:
\(\alpha \perp \beta, MA \perp \alpha, MB \perp \beta, C \in \alpha \cap (ABM), AM = m, BM = n\).
Доказать: \(ACBM\) — прямоугольник.
Найти: \(CM\).
Решение:
Четырехугольник \(ACBM\) лежит в одной плоскости. Угол \(\angle BCA\) — линейный угол двугранного угла между плоскостями \(\alpha\) и \(\beta\), \(\angle BCA = 90^\circ\). Следовательно, \(ACBM\) — прямоугольник (три угла по \(90^\circ\)).
Диагональ прямоугольника \(CM\) по теореме Пифагора:
\(
CM = \sqrt{AM^2 + BM^2} = \sqrt{m^2 + n^2}.
\)
Ответ:
\(CM = \sqrt{m^2 + n^2}\).
Начнем с анализа условий задачи. Мы имеем две плоскости \(\alpha\) и \(\beta\), которые перпендикулярны друг другу. Прямые \(MA\) и \(MB\) перпендикулярны своим плоскостям \(\alpha\) и \(\beta\) соответственно. Это значит, что точки \(A\) и \(B\) находятся на пересечении этих прямых с плоскостями.
Точка \(C\) лежит на пересечении плоскости \(\alpha\) и плоскости, содержащей треугольник \(ABM\). Это означает, что \(C\) является общей точкой для плоскостей, и угол \(\angle BCA\) является линейным углом двугранного угла между плоскостями \(\alpha\) и \(\beta\). Поскольку эти плоскости перпендикулярны, \(\angle BCA = 90^\circ\).
Теперь рассмотрим четырехугольник \(ACBM\). Из-за того, что \(\angle BCA = 90^\circ\), и учитывая, что \(MA\) и \(MB\) также перпендикулярны своим плоскостям, остальные углы в четырехугольнике \(ACBM\) также равны \(90^\circ\). Это делает \(ACBM\) прямоугольником, так как все его углы прямые.
Для нахождения диагонали \(CM\) прямоугольника \(ACBM\) используем теорему Пифагора. Поскольку \(AM = m\) и \(BM = n\), диагональ \(CM\) равна:
\(CM = \sqrt{AM^2 + BM^2} = \sqrt{m^2 + n^2}\).
Таким образом, мы доказали, что \(ACBM\) является прямоугольником и нашли длину его диагонали \(CM\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.