
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 180 Атанасян — Подробные Ответы
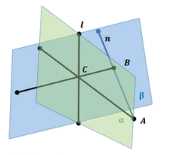
Докажите, что плоскость \(\alpha\) и не лежащая в ней прямая, перпендикулярные к одной и той же плоскости, параллельны
Дано: \( l \subset \alpha, \, \beta, \, \alpha \perp \beta \)
\( n \perp \beta, \, n \perp \alpha \)
Доказать: \( n \parallel \alpha \)
Решение:
Докажем от противного.
Пусть \( n \not\parallel \alpha \), тогда существует точка \( A \in n \), такая что \( A \in n \cap \alpha \).
Проведем из точки \( B \), принадлежащей прямой \( l \), перпендикуляр \( BC \) к прямой \( l \), где \( C \in l \).
Так как \( AC \subset \alpha \), \( BC \subset \beta \), а \( \alpha \perp \beta \), то отсюда следует, что \( AC \perp BC \).
Таким образом, из точки \( A \), лежащей вне прямой \( BC \), проведены две перпендикулярные прямые: \( n \) и \( AC \). Однако это противоречит теореме о перпендикуляре, которая утверждает, что из любой точки, не лежащей на данной прямой, можно провести к этой прямой только один перпендикуляр.
Противоречие с предположением, что \( n \not\parallel \alpha \).
Следовательно, \( n \parallel \alpha \).
Ответ: \( n \parallel \alpha \).
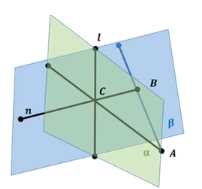
Дано: \( l \subset \alpha, \beta, \alpha \perp \beta \) и \( n \perp \beta, n \perp \alpha \). Требуется доказать, что \( n \parallel \alpha \).
Для доказательства используем метод от противного. Предположим, что \( n \not\parallel \alpha \). Это означает, что \( n \) пересекает плоскость \( \alpha \), то есть существует точка \( A \), которая принадлежит как прямой \( n \), так и плоскости \( \alpha \). Таким образом, \( A \in n \cap \alpha \).
Теперь проведем из точки \( B \), лежащей на прямой \( l \), перпендикуляр \( BC \) к прямой \( l \). Точка \( C \) при этом принадлежит прямой \( l \), то есть \( C \in l \).
Так как \( AC \subset \alpha \), а \( BC \subset \beta \), и при этом \( \alpha \perp \beta \), следует, что \( AC \perp BC \).
Таким образом, из точки \( A \), лежащей вне прямой \( BC \), к этой прямой проведены две перпендикулярные прямые: \( AC \) (лежащая в плоскости \( \alpha \)) и \( n \) (которая по условию перпендикулярна \( \beta \)). Однако это противоречит теореме о перпендикуляре, так как из любой точки, не лежащей на прямой, можно провести к этой прямой только один перпендикуляр.
Следовательно, наше предположение о том, что \( n \not\parallel \alpha \), неверно. Это доказывает, что \( n \parallel \alpha \).
Ответ: \( n \parallel \alpha \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!