ГДЗ по Геометрии 10 класс Номер 18 Атанасян — Подробные Ответы

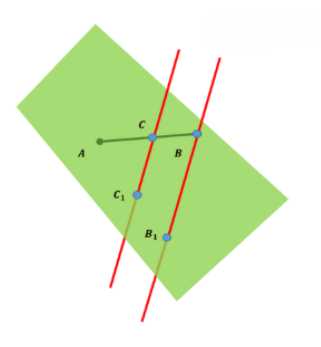
Точка \(C\) лежит на отрезке \(AB\). Через точку \(A\) проведена плоскость, а через точки \(B\) и \(C\) — параллельные прямые, пересекающие эту плоскость соответственно в точках \(B_1\) и \(C_1\). Найдите длину отрезка \(CC_1\), если:
a) точка \(C\) — середина отрезка \(AB\) и \(BB_1 = 7 \, \text{см}\);
b) \(AC : CB = 3 : 2\) и \(BB_1 = 20 \, \text{см}\).

Рассмотрим подобие треугольников \(\triangle ACC_1 \sim \triangle ABB_1\), из которого следует, что:
\(
\frac{CC_1}{BB_1} = \frac{AC}{AB}.
\)

a) Если \(C\) — середина \(AB\), то \(AC = CB = \frac{AB}{2}\). Тогда:
\(
CC_1 = BB_1 \cdot \frac{AC}{AB} = BB_1 \cdot \frac{\frac{AB}{2}}{AB} = BB_1 \cdot \frac{1}{2}.
\)

Подставляя \(BB_1 = 7 \, \text{см}\), получаем:
\(
CC_1 = 7 \cdot \frac{1}{2} = 3.5 \, \text{см}.
\)

b) Если \(AC : CB = 3 : 2\), то \(AC = \frac{3}{5} \cdot AB\). Тогда:

\(
CC_1 = BB_1 \cdot \frac{AC}{AB} = BB_1 \cdot \frac{\frac{3}{5} \cdot AB}{AB} = BB_1 \cdot \frac{3}{5}.
\)

Подставляя \(BB_1 = 20 \, \text{см}\), получаем:
\(
CC_1 = 20 \cdot \frac{3}{5} = 12 \, \text{см}.
\)

Ответы:
\(
\text{а) } CC_1 = 3.5 \, \text{см}, \quad \text{б) } CC_1 = 12 \, \text{см}.
\)

Рассмотрим задачу. Из условия известно, что \(CC_1 \parallel BB_1\), а также \(\triangle ACC_1 \sim \triangle ABB_1\) по двум равным углам (вертикальные углы и углы при основании). Воспользуемся свойством подобия треугольников для нахождения \(CC_1\).

a) Если \(C\) — середина отрезка \(AB\), то \(AC = CB = \frac{AB}{2}\). Пусть \(AB = k\), тогда \(AC = CB = \frac{k}{2}\). По свойству подобия треугольников:
\(
\frac{CC_1}{BB_1} = \frac{AC}{AB}.
\)
Подставим значения:
\(
CC_1 = BB_1 \cdot \frac{AC}{AB} = BB_1 \cdot \frac{\frac{k}{2}}{k} = BB_1 \cdot \frac{1}{2}.
\)
Учитывая, что \(BB_1 = 7 \, \text{см}\), получаем:
\(
CC_1 = 7 \cdot \frac{1}{2} = 3.5 \, \text{см}.
\)

b) Если \(AC : CB = 3 : 2\), то \(AC = \frac{3}{5} \cdot AB\), а \(CB = \frac{2}{5} \cdot AB\). По свойству подобия треугольников:
\(
\frac{CC_1}{BB_1} = \frac{AC}{AB}.
\)
Подставим значения:
\(
CC_1 = BB_1 \cdot \frac{AC}{AB} = BB_1 \cdot \frac{\frac{3}{5} \cdot AB}{AB} = BB_1 \cdot \frac{3}{5}.
\)
Учитывая, что \(BB_1 = 20 \, \text{см}\), получаем:
\(
CC_1 = 20 \cdot \frac{3}{5} = 12 \, \text{см}.
\)

Ответы:
\(
\text{а) } CC_1 = 3.5 \, \text{см}, \quad \text{б) } CC_1 = 12 \, \text{см}.
\)