Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 175 Атанасян — Подробные Ответы
Докажите, что если все рёбра тетраэдра равны, то все его двугранные углы также равны. Найдите эти углы.
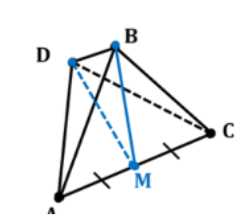
Дано: \(ABCD\) — правильный тетраэдр, все рёбра которого равны \(x\).
Пусть \(M\) — середина отрезка \(AC\). Угол \(\angle DMB\) является линейным углом двугранного угла \(BACD\).
В треугольнике \(\triangle DAC\) медиана \(DM\) равна высоте. По теореме Пифагора:
\(DM^2 + AM^2 = AD^2\).
Подставляем:
\(DM^2 + \left(\frac{x}{2}\right)^2 = x^2\),
\(DM^2 = x^2 — \frac{x^2}{4} = \frac{3x^2}{4}\),
\(DM = \frac{x\sqrt{3}}{2}\).
Аналогично, \(BM = \frac{x\sqrt{3}}{2}\).
Используем теорему косинусов в \(\triangle DMB\):
\(DB^2 = DM^2 + BM^2 — 2 \cdot DM \cdot BM \cdot \cos(\angle DMB)\).
Подставляем:
\(x^2 = \left(\frac{x\sqrt{3}}{2}\right)^2 + \left(\frac{x\sqrt{3}}{2}\right)^2 — 2 \cdot \frac{x\sqrt{3}}{2} \cdot \frac{x\sqrt{3}}{2} \cdot \cos(\angle DMB)\).
Упрощаем:
\(x^2 = \frac{3x^2}{4} + \frac{3x^2}{4} — \frac{3x^2}{2} \cdot \cos(\angle DMB)\),
\(x^2 = \frac{3x^2}{2} — \frac{3x^2}{2} \cdot \cos(\angle DMB)\).
Выражаем \(\cos(\angle DMB)\):
\(\cos(\angle DMB) = \frac{1}{3}\).
Ответ: \(\cos(\angle DMB) = \frac{1}{3}\), \(\angle DMB = \arccos\left(\frac{1}{3}\right)\).
Дано, что все ребра тетраэдра \(ABCD\) равны. Необходимо доказать, что все двугранные углы тетраэдра равны, а также найти двугранный угол \(BACD\).
Для начала строим точку \(M\) на отрезке \(AC\) так, чтобы \(AM = MC\). Это делается для упрощения вычислений, поскольку точка \(M\) является серединой отрезка \(AC\). Угол \(\angle DMB\) определяется как линейный угол двугранного угла \(BACD\).
Все стороны тетраэдра равны, поэтому все линейные углы двугранных углов тетраэдра будут одинаковыми. Чтобы доказать это, достаточно найти один из таких углов.
Обозначим длину стороны тетраэдра через \(x\). Рассмотрим треугольники \(\triangle ADC\) и \(\triangle ABC\), которые равнобедренные, поскольку все стороны тетраэдра равны. Медианы \(DM\) и \(BM\), проведенные к основанию \(AC\), являются высотами, то есть \(DM \perp AC\) и \(BM \perp AC\).
Теперь используем теорему Пифагора для вычисления длины медианы \(DM\). В прямоугольном треугольнике \(\triangle DAM\):
\(DM^2 + AM^2 = AD^2\).
Подставляем значения:
\(DM^2 + \left(\frac{x}{2}\right)^2 = x^2\).
Рассчитываем:
\(DM^2 + \frac{x^2}{4} = x^2\).
\(DM^2 = x^2 — \frac{x^2}{4}\).
\(DM^2 = \frac{3x^2}{4}\).
\(DM = \frac{x\sqrt{3}}{2}\).
Аналогично для медианы \(BM\):
\(BM = \frac{x\sqrt{3}}{2}\).
Далее используем теорему косинусов для треугольника \(\triangle DMB\):
\(DB^2 = DM^2 + BM^2 — 2 \cdot DM \cdot BM \cdot \cos(\angle DMB)\).
Подставляем известные значения:
\(x^2 = \left(\frac{x\sqrt{3}}{2}\right)^2 + \left(\frac{x\sqrt{3}}{2}\right)^2 — 2 \cdot \frac{x\sqrt{3}}{2} \cdot \frac{x\sqrt{3}}{2} \cdot \cos(\angle DMB)\).
Упрощаем выражение:
\(x^2 = \frac{3x^2}{4} + \frac{3x^2}{4} — \frac{3x^2}{2} \cdot \cos(\angle DMB)\).
\(x^2 = \frac{3x^2}{2} — \frac{3x^2}{2} \cdot \cos(\angle DMB)\).
Выражаем \(\cos(\angle DMB)\):
\(\frac{3x^2}{2} \cdot \cos(\angle DMB) = \frac{3x^2}{2} — x^2\).
\(\cos(\angle DMB) = \frac{\frac{3x^2}{2} — x^2}{\frac{3x^2}{2}}\).
\(\cos(\angle DMB) = \frac{1}{3}\).
Таким образом, линейный угол двугранного угла \(BACD\) равен \(\arccos\left(\frac{1}{3}\right)\).
Ответ: \(\cos(\angle DMB) = \frac{1}{3}\), \(\angle DMB = \arccos\left(\frac{1}{3}\right)\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.