Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 173 Атанасян — Подробные Ответы
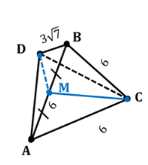
Ребро \(CD\) тетраэдра \(ABCD\) перпендикулярно к плоскости \(ABC\), \(AB = BC = AC = 6\), \(BD = \frac{3}{\sqrt{7}}\). Найдите двугранные углы \(DACB\), \(DABC\), \(BDCA\).
Дано: \(ABCD\) — тетраэдр, \(AB = BC = AC = 6\), \(BD = 3\sqrt{7}\), \(\angle(ABC, CD) = 90^\circ\).
Найти: двугранные углы \(DACB\), \(DABC\), \(BDCA\).
Решение:
Так как \(ACB \perp CD\), \(ACB \perp ACD\), \(\angle BCD = 90^\circ\), то линейный угол двугранного угла \(DACB = 90^\circ\).
Так как \(BC \perp CD\), \(AC \perp CD\), то \(\angle ACB = 60^\circ\), а значит, линейный угол двугранного угла \(BDCA = 60^\circ\).
Рассмотрим \(\triangle ABC\) и \(\triangle ABD\).
Проведем медиану \(CM\) в \(\triangle ABC\). Так как \(\triangle ABC\) равнобедренный, \(CM \perp AB\).
По теореме о трёх перпендикулярах \(AB \perp DM\), а так как \(DM\) — и медиана, и высота, \(\triangle ABD\) равнобедренный.
\(\angle CMD\) — линейный угол двугранного угла \(DABC\).
По теореме Пифагора находим \(DM\):
\(
DM = \sqrt{\frac{3 \cdot 7}{4} — 3^2} = \sqrt{54} = 3\sqrt{6}.
\)
Находим \(MC\):
\(
MC = \sqrt{6^2 — 3^2} = \sqrt{27} = 3\sqrt{3}.
\)
\(
\sin \angle CMD = \frac{DM}{MC} = \frac{3\sqrt{6}}{3\sqrt{3}} = \sqrt{2}/2, \quad \angle CMD = 45^\circ.
\)
Следовательно, двугранный угол \(DABC = 45^\circ\).
Ответ:
\(
\text{двугранный угол } DACB = 90^\circ, \quad \text{двугранный угол } BDCA = 60^\circ, \)
\(\quad \text{двугранный угол } DABC = 45^\circ.
\)
Дано: \(ABCD\) — тетраэдр, где \(AB = BC = AC = 6\), \(BD = 3\sqrt{7}\), \(\angle(ABC, CD) = 90^\circ\). Необходимо найти двугранные углы \(DACB\), \(DABC\), \(BDCA\).
Рассмотрим задачу пошагово.
Во-первых, из условия известно, что \(CD\) перпендикулярно плоскости \(\triangle ABC\). Это означает, что все углы между прямыми, лежащими в плоскости \(\triangle ABC\), и прямой \(CD\) равны \(90^\circ\). Следовательно, линейный угол двугранного угла \(DACB\) равен \(90^\circ\). Таким образом, двугранный угол \(DACB = 90^\circ\).
Во-вторых, так как \(BC \perp CD\) и \(AC \perp CD\), треугольник \(\triangle ABC\) является равносторонним с длиной стороны \(6\). Угол между сторонами \(AC\) и \(BC\) равен \(60^\circ\), что соответствует линейному углу двугранного угла \(BDCA\). Это значит, что двугранный угол \(BDCA = 60^\circ\).
Теперь рассмотрим двугранный угол \(DABC\). Для этого необходимо найти линейный угол между плоскостью \(\triangle ABC\) и плоскостью \(\triangle ABD\). Рассмотрим медиану \(CM\) в треугольнике \(\triangle ABC\). Поскольку \(\triangle ABC\) равносторонний, медиана \(CM\) перпендикулярна стороне \(AB\).
Далее проведем высоту \(DM\) в треугольнике \(\triangle ABD\). По теореме о трёх перпендикулярах, если \(AB \perp DM\) и \(AB \perp CM\), то угол \(\angle CMD\) является линейным углом двугранного угла \(DABC\).
Для нахождения угла \(\angle CMD\) сначала вычислим длину \(DM\) по теореме Пифагора в треугольнике \(\triangle ABD\).
\(
DM = \sqrt{\frac{BD^2}{4} — AB^2} = \sqrt{\frac{(3\sqrt{7})^2}{4} — 6^2} = \sqrt{\frac{63}{4} — 36} = \sqrt{\frac{63 — 144}{4}} = \sqrt{54} = \)
\(=3\sqrt{6}.
\)
Затем вычислим длину \(CM\) по теореме Пифагора в треугольнике \(\triangle ABC\):
\(
CM = \sqrt{AC^2 — \left(\frac{AB}{2}\right)^2} = \sqrt{6^2 — 3^2} = \sqrt{36 — 9} = \sqrt{27} = 3\sqrt{3}.
\)
Теперь найдём \(\sin \angle CMD\):
\(
\sin \angle CMD = \frac{DM}{CM} = \frac{3\sqrt{6}}{3\sqrt{3}} = \sqrt{2}/2.
\)
Так как \(\sin \angle CMD = \sqrt{2}/2\), то \(\angle CMD = 45^\circ\). Это означает, что двугранный угол \(DABC = 45^\circ\).
Ответ:
\(
\text{двугранный угол } DACB = 90^\circ, \quad \text{двугранный угол } BDCA = 60^\circ, \)
\(\quad \text{двугранный угол } DABC = 45^\circ.
\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.