Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 170 Атанасян — Подробные Ответы
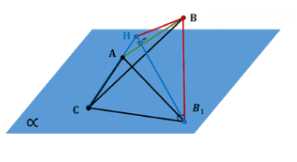
Из вершины \(B\) треугольника \(ABC\), сторона \(AC\) которого лежит в плоскости \(\alpha\), проведён к этой плоскости перпендикуляр \(BB_1\). Найдите расстояния от точки \(B\) до прямой \(AC\) и до плоскости \(\alpha\), если \(AB = 2 \, \text{см}\), \(\angle BAC = 150^\circ\) и двугранный угол \(BACB_1\) равен \(45^\circ\).
Дано:
\(A \in \alpha, C \in \alpha, B \in \alpha, B_1 \in \xi\),
\(BB_1 \perp \alpha\),
\(AB = 2 \, \text{см}\),
двугранный угол \(BACB_1 = 45^\circ\),
\(\angle BAC = 150^\circ\).
Найти: расстояние от точки \(B\) до \(AC\) и до \(\xi\) (\(BB_1\)).
Решение:
Опустим перпендикуляр из точки \(B\) на прямую \(AC\): \(BH \perp AC\).
По теореме о трёх перпендикулярах \(CH \perp AB_1\).
Рассмотрим треугольник \(\triangle ABH\) в плоскости \((ABC)\):
\(\triangle ABH\) — прямоугольный,
\(\angle BAH = 30^\circ\), так как \(\angle BAC = 150^\circ\),
\(
BH = AB \cdot \sin(30^\circ) = 2 \cdot \frac{1}{2} = 1 \, \text{см}.
\)
Рассмотрим треугольник \(\triangle BHB_1\) в плоскости \((BHB_1)\):
\(\triangle BHB_1\) — прямоугольный,
\(\angle BHB_1 = 45^\circ\) по построению, так как линейный угол двугранного угла \(BACB_1 = 45^\circ\),
\(
BB_1 = BH \cdot \sin(45^\circ) = 1 \cdot \frac{1}{\sqrt{2}} = \frac{1}{\sqrt{2}} \, \text{см}.
\)
Ответ:
\(1 \, \text{см}\) и \(\frac{1}{\sqrt{2}} \, \text{см}\).
Дано, что точка \(B\) находится в плоскости \(\alpha\), а точка \(B_1\) лежит вне этой плоскости и перпендикулярна ей (\(BB_1 \perp \alpha\)). Прямая \(AC\) лежит в плоскости \(\alpha\). Длина \(AB = 2\) см, угол между \(AB\) и \(AC\) (\(\angle BAC\)) равен \(150^\circ\), а двугранный угол между плоскостью \((ABC)\) и плоскостью \((BB_1C)\) равен \(45^\circ\). Нужно найти расстояние от точки \(B\) до прямой \(AC\) и до плоскости \(\xi\), где \(\xi\) — плоскость, перпендикулярная \(\alpha\).
Рассмотрим расстояние от точки \(B\) до прямой \(AC\). Для этого опустим перпендикуляр \(BH\) из точки \(B\) на прямую \(AC\). По теореме о трёх перпендикулярах, если \(BB_1 \perp \alpha\), то проекция \(BH\) также будет перпендикулярна прямой \(AC\).
Рассмотрим треугольник \(\triangle ABH\), лежащий в плоскости \((ABC)\). Этот треугольник прямоугольный, так как \(BH \perp AC\). Угол \(\angle BAH\) равен \(30^\circ\), так как он является смежным с углом \(\angle BAC = 150^\circ\) (\(180^\circ — 150^\circ = 30^\circ\)). Используем свойства прямоугольного треугольника, чтобы найти длину \(BH\):
\(
BH = AB \cdot \sin(30^\circ)
\)
Подставляем данные:
\(
BH = 2 \cdot \frac{1}{2} = 1 \, \text{см}
\)
Таким образом, расстояние от точки \(B\) до прямой \(AC\) равно \(1\) см.
Теперь найдём расстояние от точки \(B\) до плоскости \(\xi\). Рассмотрим треугольник \(\triangle BHB_1\), который лежит в плоскости \((BHB_1)\). Этот треугольник также прямоугольный, так как \(BB_1 \perp \alpha\), а \(BH \perp AC\). Угол \(\angle BHB_1\) равен \(45^\circ\), так как это линейный угол двугранного угла \(BACB_1\), равного \(45^\circ\). Используем свойства прямоугольного треугольника, чтобы найти длину \(BB_1\):
\(
BB_1 = BH \cdot \sin(45^\circ)
\)
Подставляем данные:
\(
BB_1 = 1 \cdot \frac{1}{\sqrt{2}} = \frac{1}{\sqrt{2}} \, \text{см}
\)
Таким образом, расстояние от точки \(B\) до плоскости \(\xi\) равно \(\frac{1}{\sqrt{2}}\) см.
Ответ: \(1\) см и \(\frac{1}{\sqrt{2}}\) см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.