
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 169 Атанасян — Подробные Ответы
Даны два двугранных угла, у которых одна грань общая, а две другие грани являются различными полуплоскостями одной плоскости. Докажите, что сумма этих двугранных углов равна \(180^\circ\).
Дано: \( \alpha \perp \beta, MN = \alpha \cap \beta \).
Доказать: сумма двугранных углов, образованных полуосями плоскости \( \beta \) и полуосью плоскости \( \alpha \), равна \( 180^\circ \).
Решение:
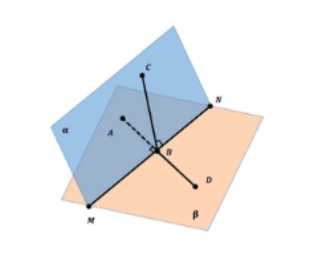
Возьмем точку \( A: A \in \beta, A \in MN \). Построим \( AD \perp MN: B \in MN \). Через точку \( B \) в плоскости \( \alpha \) построим \( CB \perp MN: C \in \alpha \). По построению с одной стороны \( \angle ABC \) и \( \angle DBC \) — линейные углы требуемых двугранных углов, а с другой стороны они лежат в одной плоскости: \( AD \cup BC \) и являются смежными. Так как сумма смежных углов равна \( 180^\circ \), утверждение доказано.
Ответ: сумма двугранных углов, образованных полуосями плоскости \( \beta \) и полуосью плоскости \( \alpha \), равна \( 180^\circ \).
Дано: \( \alpha \perp \beta \), \( MN = \alpha \cap \beta \). Требуется доказать, что сумма двугранных углов, образованных полуосями плоскости \( \beta \) и полуосью плоскости \( \alpha \), равна \( 180^\circ \).
Для доказательства выберем точку \( A \), которая принадлежит плоскости \( \beta \) и прямой \( MN \), то есть \( A \in \beta \) и \( A \in MN \). Через эту точку \( A \) проведем прямую \( AD \), перпендикулярную \( MN \), так что \( AD \perp MN \), где точка \( D \) лежит в плоскости \( \beta \).
Теперь рассмотрим точку \( B \), которая также принадлежит прямой пересечения \( MN \). Через эту точку \( B \) в плоскости \( \alpha \) проведем прямую \( CB \), перпендикулярную \( MN \), так что \( CB \perp MN \), где точка \( C \) лежит в плоскости \( \alpha \).
В результате построения мы получили два линейных угла: \( \angle ABC \) и \( \angle DBC \). Эти углы являются линейными углами двугранных углов, которые нужно рассмотреть. Угол \( \angle ABC \) соответствует двугранному углу между полуосями плоскости \( \beta \), а угол \( \angle DBC \) — двугранному углу между полуосями плоскости \( \alpha \).
Заметим, что прямые \( AD \) и \( BC \) лежат в одной плоскости и являются смежными. Это значит, что сумма углов \( \angle ABC \) и \( \angle DBC \) равна \( 180^\circ \), так как сумма смежных углов всегда равна \( 180^\circ \).
Таким образом, доказано, что сумма двугранных углов, образованных полуосями плоскости \( \beta \) и полуосью плоскости \( \alpha \), равна \( 180^\circ \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!