Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 168 Атанасян — Подробные Ответы
Двугранный угол равен \(\varphi\). На одной грани этого угла лежит точка, удалённая на расстояние \(d\) от плоскости другой грани. Найдите расстояние от этой точки до ребра двугранного угла.
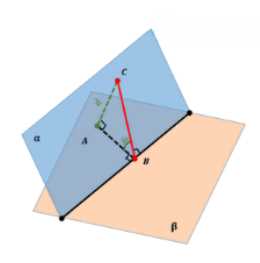
Дано: \( \alpha \perp \beta \), \( C \in \alpha \), \( \angle (\alpha, \beta) = \varphi \), \( CA = d \), \( AB \perp \alpha \cap \beta \), \( AC \perp \beta \).
Найти: \( BC \).
Решение:
По теореме о трёх перпендикулярах:
\( AB \perp \alpha \cap \beta \), \( AC \perp \alpha \cap \beta \) \(\Rightarrow\) \( CB \perp \alpha \cap \beta \).
\( CB \perp \alpha \cap \beta \Rightarrow CB \) — расстояние до прямой \( AB \).
Рассмотрим треугольник \( \triangle CBA \), он прямоугольный, \( CB \) — гипотенуза.
\(
\sin(\varphi) = \frac{AC}{BC} \Rightarrow BC = \frac{d}{\sin(\varphi)}
\)
Ответ: \( BC = \frac{d}{\sin(\varphi)} \).
Дано, что плоскости \(\alpha\) и \(\beta\) пересекаются под углом \(\varphi\), точка \(C\) лежит в плоскости \(\alpha\), а прямая \(AB\) перпендикулярна линии пересечения плоскостей \(\alpha \cap \beta\). Также известно, что отрезок \(CA\) перпендикулярен плоскости \(\beta\), а его длина равна \(d\). Необходимо найти длину отрезка \(BC\).
Рассмотрим следующее. Прямая \(AB\) перпендикулярна линии пересечения \(\alpha \cap \beta\), а отрезок \(CA\) перпендикулярен плоскости \(\beta\). По теореме о трёх перпендикулярах из этого следует, что прямая \(CB\) также перпендикулярна линии пересечения \(\alpha \cap \beta\). Таким образом, \(CB\) является расстоянием от точки \(C\) до прямой \(AB\).
Теперь рассмотрим треугольник \(CBA\). Этот треугольник прямоугольный, так как угол между \(CA\) и \(CB\) прямой по условию. В данном треугольнике гипотенуза — это сторона \(CB\), а катет \(CA\) известен и равен \(d\).
Используем определение синуса угла \(\varphi\) в прямоугольном треугольнике:
\(
\sin(\varphi) = \frac{\text{противолежащий катет}}{\text{гипотенуза}}
\)
В нашем случае противолежащий катет — это \(CA\), а гипотенуза — это \(CB\). Тогда:
\(
\sin(\varphi) = \frac{CA}{CB}
\)
Выразим \(CB\) из этой формулы:
\(
CB = \frac{CA}{\sin(\varphi)}
\)
Подставим значение \(CA = d\):
\(
CB = \frac{d}{\sin(\varphi)}
\)
Таким образом, длина отрезка \(BC\) равна \(\frac{d}{\sin(\varphi)}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.