Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 167 Атанасян — Подробные Ответы
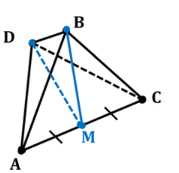
В тетраэдре \(DABC\) все рёбра равны, точка \(M\) — середина ребра \(AC\). Докажите, что \(\angle DMB\) — линейный угол двугранного угла \(BACD\).
Дано: \(ABCD\) — правильный тетраэдр, \(AM = MC\).
Доказать: \(\angle DMB\) — линейный угол двугранного угла \(BACD\).
Решение:
\(\triangle ADC\) и \(\triangle ABC\) — равнобедренные по условию, следовательно, медианы \(DM\) и \(BM\), проведённые к основанию \(AC\), являются высотами.
\(
DM \perp AC, \, BM \perp AC, \, M \in AC
\)
По определению, \(\angle DMB\) — линейный угол двугранного угла \(BACD\).
Ответ: \(\angle DMB\) — линейный угол двугранного угла \(BACD\) по определению.
Дано, что \(ABCD\) — правильный тетраэдр, а \(AM = MC\). Это означает, что все грани тетраэдра являются равносторонними треугольниками. Также медиана \(AM\) делит сторону \(AC\) пополам.
Необходимо доказать, что угол \(\angle DMB\) является линейным углом двугранного угла \(BACD\).
Рассмотрим треугольники \(\triangle ADC\) и \(\triangle ABC\). Так как \(ABCD\) — правильный тетраэдр, эти треугольники равнобедренные, и их медианы \(DM\) и \(BM\), проведённые к общей стороне \(AC\), одновременно являются высотами. Это следует из того, что медианы в равнобедренных треугольниках, проведённые к основанию, перпендикулярны ему. Таким образом, \(DM \perp AC\) и \(BM \perp AC\).
Точка \(M\) принадлежит стороне \(AC\), так как \(AM = MC\), то есть медианы пересекаются в точке \(M\), которая делит основание пополам.
Линейный угол двугранного угла \(BACD\) определяется как угол между высотами двух треугольников \(\triangle ADC\) и \(\triangle ABC\), проведёнными к их общей стороне \(AC\). В данном случае высотами являются \(DM\) и \(BM\). Следовательно, угол \(\angle DMB\) по определению является линейным углом двугранного угла \(BACD\).
Ответ: \(\angle DMB\) — линейный угол двугранного угла \(BACD\) по определению.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.