
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 166 Атанасян — Подробные Ответы
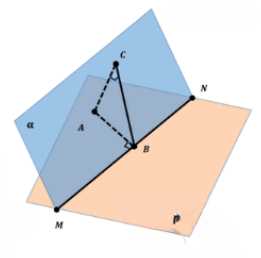
Неперпендикулярные плоскости \(\alpha\) и \(\beta\) пересекаются по прямой \(MN\). В плоскости \(\beta\) из точки \(A\) проведён перпендикуляр \(AB\) к прямой \(MN\) и из той же точки \(A\) проведён перпендикуляр \(AC\) к плоскости \(\alpha\). Докажите, что \(\angle ABC\) — линейный угол двугранного угла \(AMNC\).
Дано: \( \alpha \# \beta \), \( A, B, C \in \alpha \), \( MN \subset \alpha \cap \beta \), \( AB \perp MN \), \( AC \perp \alpha \).
Доказать: \( \angle ABC \) — линейный угол двугранного угла \( AMNC \).
Решение:
\( AC \perp \alpha \Rightarrow AB \) — наклонная к \( \alpha \), \( CB \) — её проекция.
\( AB \perp MN \), \( AC \perp \alpha \Rightarrow CB \perp MN \) (обратная теорема о трёх перпендикулярах).
Таким образом, \( AB \perp MN \), \( CB \perp MN \), следовательно, \( \angle ABC \) — линейный угол двугранного угла \( AMNC \) по определению.
Ответ: \( \angle ABC \) — линейный угол двугранного угла \( AMNC \).
Дано: \( \alpha \# \beta \), \( A, B, C \in \alpha \), \( MN \subset \alpha \cap \beta \), \( AB \perp MN \), \( AC \perp \alpha \). Необходимо доказать, что \( \angle ABC \) является линейным углом двугранного угла \( AMNC \).
Рассмотрим по шагам.
Сначала отметим, что \( AC \perp \alpha \). Это означает, что прямая \( AC \) перпендикулярна плоскости \( \alpha \). Следовательно, \( AB \) является наклонной по отношению к плоскости \( \alpha \), а её проекция на эту плоскость — это отрезок \( CB \).
Так как \( AB \perp MN \) и \( AC \perp \alpha \), то из обратной теоремы о трёх перпендикулярах следует, что \( CB \perp MN \). Обратная теорема о трёх перпендикулярах утверждает: если наклонная пересекает плоскость, а её основание соединено с точкой на прямой, перпендикулярной наклонной, то проекция наклонной также будет перпендикулярна этой прямой.
Теперь у нас есть два условия: \( AB \perp MN \) и \( CB \perp MN \). Это означает, что угол \( \angle ABC \), образованный наклонной \( AB \) и её проекцией \( CB \), соответствует определению линейного угла двугранного угла \( AMNC \). Линейный угол двугранного угла определяется как угол между двумя перпендикулярами, проведёнными в соответствующих плоскостях к линии их пересечения.
Таким образом, \( \angle ABC \) является линейным углом двугранного угла \( AMNC \).
Ответ: \( \angle ABC \) — линейный угол двугранного угла \( AMNC \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!