ГДЗ по Геометрии 10 класс Номер 164 Атанасян — Подробные Ответы

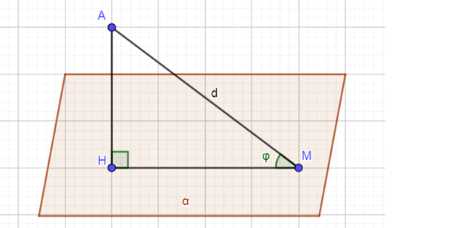
Под углом \(\varphi\) к плоскости \(\alpha\) проведена наклонная. Найдите \(\varphi\), если известно, что проекция наклонной вдвое меньше самой наклонной.

Дано: \(AM\) — наклон к \(\alpha\), \(MA\) — проекция \(AM\), \(\varphi = \angle AM\alpha\), \(AM = 2MH\). Найти: \(\varphi\).

Решение: угол между прямой и плоскостью — это угол между прямой и её проекцией на эту плоскость, то есть \(\varphi = \angle AM\alpha = \angle AMH\). Рассмотрим \(\triangle AMH\): \(\angle AMH = 90^\circ\) (так как \(AH \perp \alpha\)), \(AM = 2MH\), следовательно \(\cos \angle AMH = \frac{MH}{AM} = \frac{1}{2}\). \(\cos \angle AMH = \frac{1}{2} = \cos 60^\circ \Rightarrow \angle AMH = 60^\circ\).

Ответ: \(\varphi = 60^\circ\).

Дано: \(AM\) — наклон к плоскости \(\alpha\), \(MA\) — проекция \(AM\) на плоскость \(\alpha\), угол \(\varphi = \angle AM\alpha\), \(AM = 2MH\). Требуется найти угол \(\varphi\).

Рассуждение начинается с определения угла между прямой и плоскостью. Угол между прямой и плоскостью — это угол между прямой и её проекцией на эту плоскость. В данном случае прямая \(AM\) наклонена к плоскости \(\alpha\), а её проекция на эту плоскость — это отрезок \(MA\). Следовательно, угол \(\varphi\) между прямой \(AM\) и плоскостью \(\alpha\) равен углу между прямой \(AM\) и её проекцией \(MA\), то есть \(\varphi = \angle AMH\).

Рассмотрим прямоугольный треугольник \(\triangle AMH\), где \(\angle AMH = 90^\circ\), так как \(AH\) перпендикулярен плоскости \(\alpha\). По условию \(AM = 2MH\). Используя это соотношение, можно найти косинус угла \(\angle AMH\):
\(
\cos \angle AMH = \frac{MH}{AM}.
\)
Подставляем известные значения:
\(
\cos \angle AMH = \frac{MH}{2MH} = \frac{1}{2}.
\)

По таблице значений тригонометрических функций известно, что \(\cos 60^\circ = \frac{1}{2}\). Следовательно, \(\angle AMH = 60^\circ\).

Таким образом, угол \(\varphi = \angle AM\alpha = 60^\circ\).

Ответ: \(\varphi = 60^\circ\).