
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 162 Атанасян — Подробные Ответы
Прямая \(MA\) проходит через точку \(A\) плоскости \(\alpha\) и образует с этой плоскостью угол \(\varphi_0 \neq 90^\circ\). Докажите, что \(\varphi_0\) является наименьшим из всех углов, которые прямая \(MA\) образует с прямыми, проведёнными в плоскости \(\alpha\) через точку \(A\).
Решение:
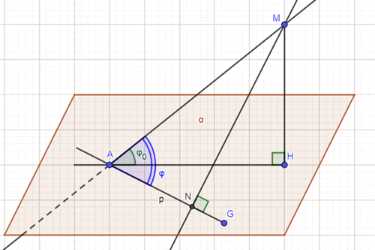
Обозначим буквой \(H\) основание перпендикуляра, проведённого из точки \(M\) к плоскости \(\alpha\), и рассмотрим произвольную прямую \(p\) в плоскости \(\alpha\), проходящую через точку \(A\) и отличную от прямой \(AH\). Угол между прямыми \(AM\) и \(p\) обозначим через \(\varphi\) (рис. 57) и докажем, что \(\varphi > \varphi_0\). Из точки \(M\) проведём перпендикуляр \(MN\) к прямой \(p\). Если точка \(N\) совпадает с точкой \(A\), то \(\varphi = 90^\circ\) и поэтому \(\varphi > \varphi_0\). Рассмотрим случай, когда точки \(A\) и \(N\) не совпадают (см. рис. 57). Отрезок \(AM\) — общая гипотенуза прямоугольных треугольников \(ANM\) и \(AHM\), поэтому \(\sin \varphi = \frac{MN}{AM}\), \(\sin \varphi_0 = \frac{MH}{AM}\). Так как \(MN > MH\) (\(MN\) — наклонная, \(MH\) — перпендикуляр), то из этих равенств следует, что \(\sin \varphi > \sin \varphi_0\), и поэтому \(\varphi > \varphi_0\).
Дано: прямая \(MA\) проходит через точку \(A\) плоскости \(\alpha\) и образует с этой плоскостью угол \(\varphi_0 \neq 90^\circ\).
Доказать: \(\varphi_0\) — наименьший из всех углов, которые прямая \(MA\) образует с прямыми, проведенными в плоскости \(\alpha\) через точку \(A\).
Обозначим основание перпендикуляра из точки \(M\) к плоскости \(\alpha\) буквой \(H\). Рассмотрим произвольную прямую \(p\) в плоскости \(\alpha\), проходящую через точку \(A\) и отличную от прямой \(AH\). Угол между прямыми \(AM\) и \(p\) обозначим \(\varphi\) и докажем, что \(\varphi > \varphi_0\).
Проведем перпендикуляр \(MN\) из точки \(M\) к прямой \(p\). Если \(N = A\), то \(\varphi = 90^\circ\), следовательно, \(\varphi > \varphi_0\).
Если \(N \neq A\), то в прямоугольных треугольниках \(ANM\) и \(AHM\) гипотенуза общая (\(AM\)), а \(MN > MH\) (так как \(MN\) — наклонная, а \(MH\) — перпендикуляр).
Из этого следует, что \(\sin \varphi = \frac{MN}{AM} > \frac{MH}{AM} = \sin \varphi_0\), а значит, \(\varphi > \varphi_0\).
Таким образом, \(\varphi_0\) — минимальный угол, что и требовалось доказать.
Дано: прямая \(MA\) проходит через точку \(A\) плоскости \(\alpha\) и образует с этой плоскостью угол \(\varphi_0 \neq 90^\circ\). Требуется доказать, что \(\varphi_0\) является наименьшим из всех углов, которые прямая \(MA\) образует с прямыми, проведенными в плоскости \(\alpha\) через точку \(A\).
Для доказательства обозначим буквой \(H\) основание перпендикуляра, опущенного из точки \(M\) на плоскость \(\alpha\). Рассмотрим произвольную прямую \(p\), лежащую в плоскости \(\alpha\) и проходящую через точку \(A\), которая отличается от прямой \(AH\). Обозначим угол между прямыми \(AM\) и \(p\) через \(\varphi\). Нам нужно доказать, что \(\varphi > \varphi_0\).
Проведем из точки \(M\) перпендикуляр \(MN\) к прямой \(p\). Рассмотрим два случая:
Первый случай: если точка \(N\) совпадает с точкой \(A\), то угол \(\varphi = 90^\circ\). Так как \(\varphi_0 \neq 90^\circ\), то очевидно, что \(\varphi > \varphi_0\).
Второй случай: если точки \(A\) и \(N\) не совпадают. В этом случае рассмотрим прямоугольные треугольники \(ANM\) и \(AHM\). В этих треугольниках отрезок \(AM\) является общей гипотенузой. Поскольку \(MN > MH\) (так как \(MN\) — наклонная, а \(MH\) — перпендикуляр), то выполняется неравенство \(\frac{MN}{AM} > \frac{MH}{AM}\). Это означает, что \(\sin \varphi > \sin \varphi_0\).
Так как функция \(\sin x\) возрастает на интервале \((0^\circ, 90^\circ)\), то из неравенства \(\sin \varphi > \sin \varphi_0\) следует, что \(\varphi > \varphi_0\).
Таким образом, угол \(\varphi_0\) является наименьшим из всех углов, которые прямая \(MA\) образует с прямыми, лежащими в плоскости \(\alpha\) и проходящими через точку \(A\). Это и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!