Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 161 Атанасян — Подробные Ответы
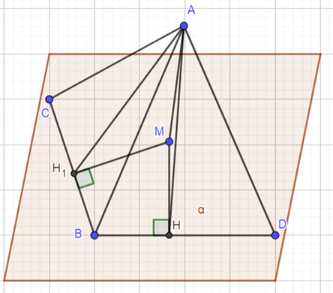
Луч \(BA\) не лежит в плоскости неразвёрнутого угла \(CBD\). Докажите, что если \(\angle ABC = \angle ABD\), причём \(\angle ABC < 90^\circ\), то проекцией луча \(BA\) на плоскость \(CBD\) является биссектриса угла \(CBD\).
Дано: \(BA \in \angle CBD\); \(\angle ABC < 90^\circ\); \(\angle ABC = \angle ABD\).
Доказать: проекция \(BA\) на \(\triangle CBD\) — биссектриса \(\angle CBD\). Построим \(AM \perp \alpha\). В плоскости \(\alpha\) построим \(MH\) и \(MH_1\), перпендикулярные \(BD\) и \(BC\) соответственно.
\(HM \perp BD\) и \(H_1M \perp CB\), следовательно, \(AH_1 \perp CB\), \(AH \perp BD\) (по теореме о трёх перпендикулярах).
Рассмотрим \(\triangle ABH\) и \(\triangle ABH_1\) — прямоугольные. \(\angle ABH_1 = \angle ABH\), \(AB\) — общая сторона, значит, \(\triangle ABH = \triangle ABH_1\) (по гипотенузе и острому углу), отсюда \(BH = BH_1\).
В плоскости \(\alpha\) построим \(BM\) — проекцию \(AB\).
Рассмотрим \(\triangle BMH\) и \(\triangle BMH_1\) — прямоугольные. \(BM\) — общая, \(BH = BH_1\), \(\triangle BMH = \triangle BMH_1\) (по углу и двум сторонам), отсюда \(\angle MBH = \angle MBH_1\) (как соответствующие элементы в равных фигурах).
\(\angle CBD = 2 \cdot \angle MBH = 2 \cdot \angle MBH_1\), следовательно, \(BM\) — биссектриса \(\angle DCB\), что и требовалось доказать.
Дано, что \(BA \in \angle CBD\), \(\angle ABC < 90^\circ\) и \(\angle ABC = \angle ABD\). Требуется доказать, что проекция \(BA\) на плоскость \(\triangle CBD\) является биссектрисой угла \(\angle CBD\). Сначала строим прямую \(AM\), перпендикулярную плоскости \(\alpha\), где \(\alpha\) — плоскость \(\triangle CBD\). Это позволяет нам работать с проекциями отрезков на плоскость \(\alpha\). В плоскости \(\alpha\) строим две перпендикуляра: \(MH \perp BD\) и \(MH_1 \perp BC\). Таким образом, \(MH\) и \(MH_1\) являются высотами, опущенными из точки \(M\) на стороны треугольника \(\triangle CBD\). Так как \(MH \perp BD\) и \(MH_1 \perp BC\), то по теореме о трёх перпендикулярах \(AH \perp BD\) и \(AH_1 \perp BC\). Это означает, что \(AH\) и \(AH_1\) являются перпендикулярами к разным сторонам треугольника. Рассмотрим два прямоугольных треугольника \(\triangle ABH\) и \(\triangle ABH_1\). В этих треугольниках углы \(\angle ABH\) и \(\angle ABH_1\) равны, так как \(\angle ABC = \angle ABD\) по условию. Также у треугольников общая сторона \(AB\). По признаку равенства треугольников (по гипотенузе и острому углу) \(\triangle ABH = \triangle ABH_1\). Из равенства треугольников следует, что \(BH = BH_1\).
Теперь в плоскости \(\alpha\) строим \(BM\) — проекцию отрезка \(AB\). Это позволяет нам работать с проекцией \(BA\) на плоскость \(\triangle CBD\).
Рассмотрим два прямоугольных треугольника \(\triangle BMH\) и \(\triangle BMH_1\). У этих треугольников общая сторона \(BM\), а также \(BH = BH_1\) (что было доказано ранее). Кроме того, углы \(\angle MBH\) и \(\angle MBH_1\) равны, так как они лежат напротив равных сторон. По признаку равенства треугольников (по углу и двум сторонам) \(\triangle BMH = \triangle BMH_1\). Из равенства треугольников следует, что \(\angle MBH = \angle MBH_1\).
Так как \(\angle CBD = \angle MBH + \angle MBH_1\) и \(\angle MBH = \angle MBH_1\), то \(\angle CBD = 2 \cdot \angle MBH\). Это означает, что \(BM\) делит угол \(\angle CBD\) пополам, то есть \(BM\) является биссектрисой угла \(\angle CBD\).
Таким образом, доказано, что проекция \(BA\) на плоскость \(\triangle CBD\) является биссектрисой угла \(\angle CBD\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.