ГДЗ по Геометрии 10 класс Номер 160 Атанасян — Подробные Ответы

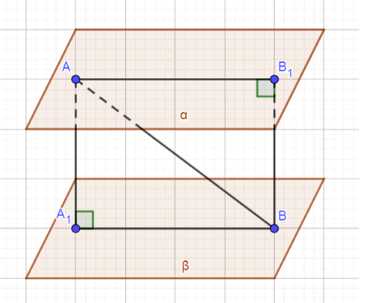
Концы отрезка \(AB\) лежат на двух параллельных плоскостях, расстояние между которыми равно \(d\), причём \(d < AB\). Докажите, что проекции отрезка \(AB\) на эти плоскости равны. Найдите эти проекции, если \(AB = 13 \, \text{см}\), \(d = 5 \, \text{см}\).

Дано: \(A \in \alpha; B \in \beta; \alpha \parallel \beta; p(\alpha, \beta) = d; AB = 13 \, \text{см}; d = 5 \, \text{см}\).

Рассмотрим проекцию \(AB\) на плоскости. \(AB_1\) — проекция \(AB\) на \(\alpha\), так как \(A \in \alpha\), следовательно, \(BB_1 \perp \alpha\). Аналогично, \(A_1B\) — проекция \(AB\) на \(\beta\), так как \(B \in \beta\), следовательно, \(AA_1 \perp \beta\).

Так как \(AA_1 \perp \beta\) и \(BB_1 \perp \alpha\), то \(AA_1 \perp BB_1\). Проекции \(AB_1 \in \alpha\) и \(A_1B \in \beta\), а \(\alpha \parallel \beta\), следовательно, \(AB_1 \parallel A_1B\).

Из условий \(AA_1 \perp BB_1\) и \(AB_1 \parallel A_1B\) следует, что \(AA_1BB_1\) — прямоугольник. По свойству прямоугольника \(A_1B = AB_1\), что и требовалось доказать.

Рассмотрим \(\triangle AA_1B\), который является прямоугольным. По теореме Пифагора:
\(
A_1B = \sqrt{AB^2 — AA_1^2} = \sqrt{13^2 — 5^2} = \sqrt{169 — 25} = 12 \, \text{см}.
\)

Ответ: \(AB_1 = A_1B = 12 \, \text{см}\).

Дано: \(A \in \alpha\), \(B \in \beta\), \(\alpha \parallel \beta\), \(p(\alpha, \beta) = d\), \(AB = 13 \, \text{см}\), \(d = 5 \, \text{см}\).

Рассмотрим проекции \(AB\) на плоскости \(\alpha\) и \(\beta\). Точка \(A\) принадлежит плоскости \(\alpha\), следовательно, проекция \(AB_1\) лежит в \(\alpha\), а \(BB_1 \perp \alpha\). Аналогично, точка \(B\) принадлежит плоскости \(\beta\), следовательно, проекция \(A_1B\) лежит в \(\beta\), а \(AA_1 \perp \beta\).

Так как \(AA_1 \perp \beta\) и \(BB_1 \perp \alpha\), то прямые \(AA_1\) и \(BB_1\) перпендикулярны друг другу. Это следует из того, что плоскости \(\alpha\) и \(\beta\) параллельны, а перпендикуляры к ним пересекаются под прямым углом.

Проекции \(AB_1\) и \(A_1B\) принадлежат параллельным плоскостям \(\alpha\) и \(\beta\). Так как \(\alpha \parallel \beta\), то прямые \(AB_1\) и \(A_1B\) также параллельны.

Из того, что \(AA_1 \perp BB_1\) и \(AB_1 \parallel A_1B\), следует, что четырёхугольник \(AA_1BB_1\) является прямоугольником. У прямоугольника противоположные стороны равны, следовательно, \(A_1B = AB_1\). Это доказывает равенство длин проекций.

Теперь рассмотрим треугольник \(AA_1B\), который является прямоугольным (по построению). В этом треугольнике гипотенуза \(AB = 13 \, \text{см}\), а один из катетов \(AA_1 = d = 5 \, \text{см}\). Найдём второй катет \(A_1B\) по теореме Пифагора:
\(A_1B = \sqrt{AB^2 — AA_1^2} = \sqrt{13^2 — 5^2} = \sqrt{169 — 25} = \sqrt{144} = 12 \, \text{см}\).

Таким образом, \(AB_1 = A_1B = 12 \, \text{см}\).