
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 159 Атанасян — Подробные Ответы
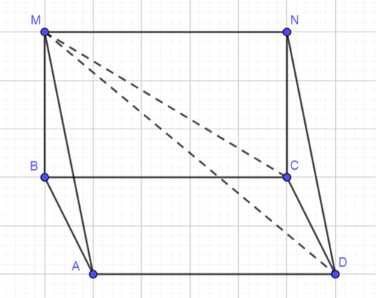
Прямая \(BM\) перпендикулярна к плоскости прямоугольника \(ABCD\). Докажите, что прямая, по которой пересекаются плоскости \(ADM\) и \(BCM\), перпендикулярна к плоскости \(ABM\)
Дано: \(ABCD\) — прямоугольник; \(BM \perp ABCD\). Доказать: \(MN \perp ABM\).
Проведём линию пересечения плоскостей: \(NC \parallel BM\) и \(NC \parallel CB\), тогда \(ABM \perp DCN\) (так как \(CN \parallel BM\), \(AB \parallel DC\)).
Проведём прямую \(ND \perp MA\), соединим точки \(M\) и \(N\), тогда \(BMC \cap MDA = NM\).
\(DN \perp MA\) и \(MA \perp DA\), следовательно, \(DN \perp DA\) (по теореме о трёх перпендикулярах).
\(DA \perp BM\) и \(DA \perp AB\), значит \(AD \perp MBA\).
\(MA \perp AD\), \(DN \perp AD\) и \(AM = AD\), следовательно, \(MNDA\) — прямоугольник, отсюда \(MN \perp AD\), значит \(MN \perp ABM\), что и требовалось доказать.
Дано: \(ABCD\) — прямоугольник, \(BM \perp ABCD\). Требуется доказать, что \(MN \perp ABM\).
Сначала определим линию пересечения плоскостей. Поскольку \(NC \parallel BM\) и \(NC \parallel CB\), это означает, что \(NC\) лежит в плоскости \(DCN\). Так как \(CN \parallel BM\) и \(AB \parallel DC\), то плоскость \(ABM\) перпендикулярна плоскости \(DCN\).
Далее проведём прямую \(ND\), которая перпендикулярна \(MA\). Соединим точки \(M\) и \(N\), тогда прямая \(NM\) будет общей для плоскостей \(BMC\) и \(MDA\). Это означает, что \(NM\) является линией их пересечения.
Рассмотрим взаимное расположение прямых \(DN\) и \(DA\). Поскольку \(DN \perp MA\) и \(MA \perp DA\), то по теореме о трёх перпендикулярах следует, что \(DN \perp DA\).
Теперь проанализируем взаимное расположение прямой \(DA\) с плоскостью \(ABM\). Поскольку \(DA \perp BM\) и \(DA \perp AB\), то \(DA \perp MBA\) (то есть перпендикулярна всей плоскости \(ABM\)).
Далее заметим, что \(MA \perp AD\), \(DN \perp AD\), а также \(AM = AD\). Это означает, что четырёхугольник \(MNDA\) является прямоугольником. Из этого следует, что \(MN \perp AD\).
\(DA \perp BM\) и \(DA \perp AB\), значит \(AD \perp MBA\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!